การสร้างภาพในคอมพิวเตอร์ก็คือการจัดการกับพิกัดจุดต่างๆ ซึ่งโดยมาก(และโดยพื้นฐาน)แล้วก็คือเราต้องการเลื่อน/ขยาย/หมุน/สะท้อนบรรดาจุดเหล่านั้นด้วยกฎเดียวกันเพื่อให้ผลลัพธ์พิกัดของทุกจุดไปอยู่ ณ ตำแหน่งที่ถูกต้องตามที่เราต้องการ ซึ่งถ้าเรายังจำกันได้จากความรู้ด้านพีชคณิตเชิงเส้น เราสามารถใช้เมทริกซ์เข้ามาช่วยคำนวณได้อย่างง่ายดาย

เพื่อความง่ายเราจะดูตัวอย่างที่สองมิติพอ นั่นคือเราจะสนใจจุดต่างๆ ที่ถูกเขียนแทนด้วยเวกเตอร์ $\vec{p}=[\;\begin{smallmatrix}x\newline y\end{smallmatrix}\;]$ ซึ่งทำให้ได้ว่า

• เลื่อนด้วยเวกเตอร์ $\vec{v}=[\;\begin{smallmatrix}a\newline b\end{smallmatrix}\;]$ (เลื่อนตามแกนนอนด้วยระยะ $a$ และเลื่อนตามแกนตั้งด้วยระยะ $b$)

  \[T_\vec{v}(\vec{p}) = \begin{bmatrix}x\\y\end{bmatrix} + \begin{bmatrix}a\\b\end{bmatrix}\]

• ขยายขนาดออกจากจุดกำเนิดอย่างเท่ากันในทุกทิศทางด้วยสเกลาร์ $s$

  \[M_s(\vec{p}) = s\begin{bmatrix}x\\y\end{bmatrix}\]

• ขยายขนาดด้วยเวกเตอร์ $\vec{v}=[\;\begin{smallmatrix}a\newline b\end{smallmatrix}\;]$ (ขยายตามแกนนอน $a$ เท่า และขยายตามแกนตั้ง $b$ เท่า)

  \[M_\vec{v}(\vec{p}) = \begin{bmatrix}a&0\\0&b\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}\]

• สะท้อนในแนวแกนนอน (หรือพูดอีกอย่างก็คือการขยายตามแกนนอนด้วยขนาดลบหนึ่งเท่า)

  \[M_{-1}^x(\vec{p}) = \begin{bmatrix}-1&0\\0&1\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}\]

• หมุนทวนเข็มนาฬิกาด้วยมุม $\theta$ รอบจุดกำเนิด

  \[R_\theta(\vec{p}) = \begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}\]

• เฉือน (shear) ตามแกนนอนด้วยความชัน $1/a$

  \[S_a^x(\vec{p}) = \begin{bmatrix}1&a\\0&1\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}\]

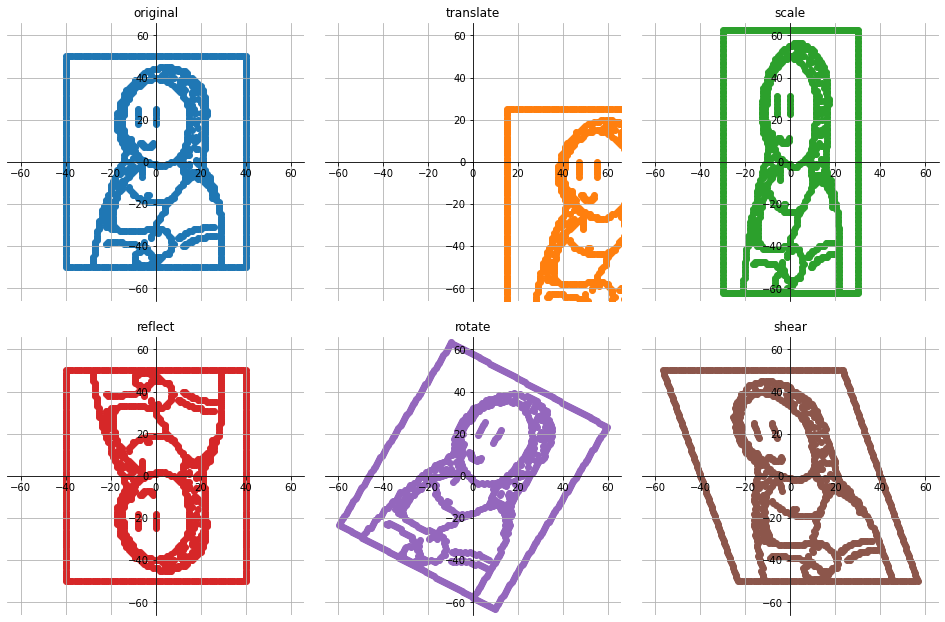
ตัวอย่างการแปลงพื้นฐานแบบต่างๆ บนภาพ Mona Lisa ขอขอบคุณภาพจาก @srakrn

ความเจ๋งของการอธิบายมันในรูปฟังก์ชันได้เช่นนี้ คือเราสามารถนำผลลัพธ์มาส่งต่อกันเป็นลูกโซ่ได้ เช่น หากเราเริ่มด้วยการเลื่อนตามแกนนอนเป็นระยะ $4$ หน่วย หลังจากนั้นหมุนด้วยมุม $30^\circ$ แล้วปิดท้ายด้วยการสะท้อนในแนวแกนตั้ง เราจะเขียนอธิบายการกระทำตามลำดับดังกล่าวออกมาเป็นสมการออกมาได้ว่า

\[{\color{blue}M_{-1}^y({\color{red}R_{30^\circ}({\color{green}T_4^x({\color{black}\vec{p}})})})} = {\color{blue}\left( \begin{bmatrix}1&0\\0&-1\end{bmatrix} {\color{red}\left( \begin{bmatrix}\cos30^\circ&-\sin30^\circ\\\sin30^\circ&\cos30^\circ\end{bmatrix} {\color{green}\left( {\color{black}\begin{bmatrix}x\\y\end{bmatrix}} + \begin{bmatrix}4\\0\end{bmatrix} \right)} \right)} \right)}\]

ยิ่งไปกว่านั้น ถ้าเรามองในแง่การรีดประสิทธิภาพโค้ด แทนที่เราจะเริ่มจากการเอาแต่ละจุด $\vec{p}$ ไปค่อยๆ ผ่านทีละฟังก์ชันไล่ย้อนกลับมา เราสามารถ “รวบ” ฟังก์ชันที่คำนวณเมทริกซ์ทั้งหมดทิ้งไว้ก่อนได้เลย นั่นคือเราจะมองการดำเนินการต่างๆ เป็นฟังก์ชันประกอบ (function composition) เช่นนี้

\[\begin{align} (M_{-1}^y \circ R_{30^\circ} \circ T_4^x)\; \vec{p} &= M_{-1}^y(R_{30^\circ}(T_4^x(\vec{p}))) \\ &= \begin{bmatrix}1&0\\0&-1\end{bmatrix} \begin{bmatrix}\sqrt3/2&-1/2\\1/2&\sqrt3/2\end{bmatrix} \left( \begin{bmatrix}x\\y\end{bmatrix} + \begin{bmatrix}4\\0\end{bmatrix} \right) \\ &= \begin{bmatrix}\sqrt3/2&-1/2\\-1/2&-\sqrt3/2\end{bmatrix} \left( \begin{bmatrix}x\\y\end{bmatrix} + \begin{bmatrix}4\\0\end{bmatrix} \right) \\ &= \begin{bmatrix}\sqrt3/2&-1/2\\-1/2&-\sqrt3/2\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix} + \begin{bmatrix}2\sqrt3\\-2\end{bmatrix} \end{align}\]

สังเกตว่าการดำเนินการแทบทุกตัวข้างต้น (ยกเว้นการเลื่อนเพียงตัวเดียวที่ไม่เหมือนเพื่อน) นั้นมีลักษณะร่วมกัน คือ มันจะนำเมทริกซ์อันหนึ่งมาคูณกับเวกเตอร์ที่เราใส่เข้าไป หรือพูดอีกอย่างก็คือผลลัพธ์มันจะอยู่ในรูป $\mathbf{A}\vec{p}$ เราเรียกการกระทำในลักษณะนี้ว่า การแปลงเชิงเส้น (linear transformation) ซึ่งมีลักษณะร่วมที่สำคัญคือทุกการกระทำมันจะต้องอ้างอิงอยู่บนจุดกำเนิดเสมอ

แต่อย่างที่เห็นว่าการเลื่อนนั้นแตกต่างจากการดำเนินการอื่น (และเมื่อนำมันมาใช้ร่วมกับการแปลงอันอื่นๆ) จะทำให้ได้ว่าเราต้องเขียนมันในรูป $\mathbf{A}\vec{p}+\vec{v}$ แทน และเราจะเปลี่ยนไปเรียกมันว่า การแปลงสัมพรรค (affine transformation) โดยความสามารถที่เพิ่มขึ้นมาก็คือเราไม่จำเป็นต้องอ้างอิงจุดกำเนิดเพียงอย่างเดียวแล้ว เช่น หากเราต้องการหมุนด้วยมุม $\theta$ รอบจุด $\vec{v}=[\;\begin{smallmatrix}a\newline b\end{smallmatrix}\;]$ เราจะเขียนได้ว่า

\[(T_\vec{v} \circ R_\theta \circ T_{-\vec{v}})\; \vec{p} = \begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix} + \begin{bmatrix} a(1 - \cos\theta) + b \sin\theta \\ b(1 - \cos\theta) - a \sin\theta \end{bmatrix}\]

ถึงตรงนี้ทุกอย่างก็ดูเข้าท่าน่าจะเอาไปใช้งานได้โดยไม่มีปัญหาแล้ว แต่ว่ามันก็ยังมีความไม่สวยอยู่ในสมการตรงที่มันติดการบวกเวกเตอร์การเลื่อนห้อยท้าย แทนที่เราจะสามารถเขียนทั้งสมการด้วยการคูณเมทริกซ์เพียงอย่างเดียว (หรือก็คือ ทำให้มันเป็นการแปลงเชิงเส้น) คำถามคือแล้วเราจะสามารถกำจัดพจน์เวกเตอร์นั้นทิ้งไปได้หรือเปล่า?

หากเรายังคิดในกรอบสองมิติเช่นเดิมก็คือทำไม่ได้ ดังนั้นเราจะเพิ่มมิติเข้าไปในข้อมูลของเราโดยอาศัยข้อสังเกตที่ว่า ถ้าเราให้ค่าประจำมิติใหม่นี้เป็นค่าคงที่ เราสามารถสร้างผลบวกขึ้นมาได้ฟรีๆ โดยการเอาเมทริกซ์ไปคูณกับค่าคงที่ในมิติใหม่นั้น

พูดอย่างเป็นสมการหน่อยก็คือ สำหรับข้อมูลสองมิติ $\vec{p}=[\;\begin{smallmatrix}x\newline y\end{smallmatrix}\;]$ เดิมที่เรามี เราจะเปลี่ยนไปเขียนด้วยเวกเตอร์สามมิติแทน ดังนี้

\[\vec{p} = \begin{bmatrix}x\\y\\1\end{bmatrix}\]

ซึ่งจะทำให้เราได้ฟังก์ชันสำหรับการแปลงเชิงเส้นที่มีหน้าตาแบบเดิม เพิ่มเติมก็คือมีแถวและหลักเพิ่มเข้ามาโดยมีค่าทุกช่องเป็นศูนย์หมดยกเว้นช่องทะแยงมุมที่มีค่าเป็นหนึ่ง เช่น การหมุนรอบจุดกำเนิดจะกลายเป็น

\[R_\theta(\vec{p}) = \begin{bmatrix}\cos\theta&-\sin\theta&0\\\sin\theta&\cos\theta&0\\0&0&1\end{bmatrix} \begin{bmatrix}x\\y\\1\end{bmatrix}\]

ส่วนการเลื่อนด้วย $\vec{v}=[\;\begin{smallmatrix}a\newline b\end{smallmatrix}\;]$ ที่เคยเป็นตัวปัญหา เราก็สามารถเปลี่ยนไปเขียนในรูปของการคูณเมทริกซ์ได้แล้วว่า

\[T_\vec{v}(\vec{p}) = \begin{bmatrix}1&0&a\\0&1&b\\0&0&1\end{bmatrix} \begin{bmatrix}x\\y\\1\end{bmatrix}\]

แน่นอนว่าเราอาจลองเช็คคำตอบดูได้ เช่น กลับไปพิจารณาการหมุนด้วยมุม $\theta$ รอบจุด $\vec{v}$ เราจะได้

\[\begin{align} (T_\vec{v} \circ R_\theta \circ T_{-\vec{v}})\; \vec{p} &= \begin{bmatrix}1&0&a\\0&1&b\\0&0&1\end{bmatrix} \begin{bmatrix}\cos\theta&-\sin\theta&0\\\sin\theta&\cos\theta&0\\0&0&1\end{bmatrix} \begin{bmatrix}1&0&-a\\0&1&-b\\0&0&1\end{bmatrix} \begin{bmatrix}x\\y\\1\end{bmatrix} \\ &= \begin{bmatrix} \cos\theta & -\sin\theta & a(1 - \cos\theta) + b \sin\theta \\ \sin\theta & \cos\theta & b(1 - \cos\theta) - a \sin\theta \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}x\\y\\1\end{bmatrix} \end{align}\]

สังเกตว่าผลลัพธ์สุดท้ายจะออกมาอยู่ในรูป $[x’\;y’\;1]^T$ เสมอ นั่นก็คือเราสามารถหยิบค่า $x’$ และ $y’$ ไปใช้งาน (เช่น พล็อตกราฟ) แบบสองมิติได้เลย โดยไม่ต้องสนใจค่าคงที่ในมิติที่เพิ่มขึ้นมาเลยก็ได้ (มันจะมีค่าเป็นหนึ่งตลอดกาล)

ดังนั้นจริงๆ แล้วการแปลงสัมพรรคในมิติที่เราสนใจ มันก็คือการแปลงเชิงเส้นในมิติที่สูงขึ้นมาอีกหนึ่งมิตินั่นเอง ซึ่งพอมันเขียนเป็นการคูณกันของเมทริกซ์เพียวๆ ได้แบบนี้แล้ว แปลว่าเราก็ไม่จำเป็นต้องพึ่งพาการเขียนด้วยฟังก์ชันอีกต่อไป เพราะเราสามารถหยิบเอาเมทริกซ์สำหรับการแปลงอันต่างๆ ที่เราสนใจมาวางเรียงต่อกันเป็นผลคูณได้เลย