$ 0! = 1 $
สัญลักษณ์คณิตศาสตร์ที่น่าฉงนปนตกใจมากที่สุดคงหนีไม่พ้น factorial ($!$) และสิ่งที่น่าตกใจยิ่งกว่าคือคำตอบที่ว่า $0!=1$ เมื่อถามต่อว่าทำไมก็จะได้รับคำตอบว่ามันเป็นนิยาม ซึ่งจริงๆ ก็ถูกต้องแล้วแหละ แต่หลายคนคงอยากให้มันมีความหมายที่ลึกซึ้งกว่านั้น
เมื่อลองพิจณานิยามพื้นฐานสุดของ factorial การจะได้มาซึ่ง $n!$ นั้นคือการหาผลคูณจาก $1$ ขึ้นไปเรื่อยๆ จนถึง $n$ การหา $1!$ ได้จึงไม่แปลก เพราะมันคือผลคูณจาก $1$ ไปจนถึง $1$ (ซึ่งก็คือไม่ต้องคูณเลยซักตัว) แต่ถ้าคิดตามนิยามนี้ $0!$ ก็ไม่มีตัวตนเพราะว่า $1$ มีค่ามากกว่า $0$ (แล้วเราจะคูณขึ้นไปเรื่อยๆ ได้ยังไง!?) ตอนนี้ถ้าเราอยากให้ $0!$ มีค่าก็ต้องหาวิธีคำนวณ/นิยายามที่มีเหตุผลขึ้นมาเพื่อให้คนอื่นยอมรับค่านั้นๆ … ซึ่งแน่นอนว่ามันไม่ใช่การเปลี่ยนนิยามข้างต้นเป็น $n!$ คือผลคูณจาก $0$ ขึ้นไปเรื่อยๆ จนถึง $n$ แน่ :P
ความพยายามแรกที่จะหาคำตอบนี้ ก็คือการกล่าวถึง factorial ในรูปของ $n!=n(n-1)!$ จะเห็นว่าสูตรนี้เป็น recursive การจะหาผลลัพท์ได้นั้น ต้องมองย้อนกลับไป 1 ขั้นเสมอ ในทำนองเดียวกัน ถ้าเรารู้ผลลัพท์ของขั้นตอนปัจจุบัน เราอาจจะสามารถย้อนกลับไปคำนวณผลลัพท์สำหรับขั้นตอนก่อนหน้าได้ ดังนั้น
\[\begin{align} 5! &= 120 &= 5 \times 4! \\ 4! &= 24 &= 4 \times 3! \\ 3! &= 6 &= 3 \times 2! \\ 2! &= 2 &= 2 \times 1! \\ 1! &= 1 &= 1 \times 0! \end{align}\]เลขตัวเดียวที่คูณหนึ่งแล้วยังได้หนึ่งก็คือหนึ่ง ดังนั้น $0!=1$ อย่างไม่ต้องสงสัย…
ใครตอบมาอย่างนี้บอกได้เลยว่าเป็นนักคณิตศาสตร์เกรด C เพราะถ้าเราลองทำต่อไปจะได้ว่า
\[0! = 1 = 0 \times (-1)!\]แน่นอนว่าสมการนี้หาคำตอบไม่ได้ (เลขใดๆ คูณศูนย์ย่อมได้ศูนย์) แม้ว่าสมการข้างต้นจะทำงานได้ดีไม่มีผิดถ้าหาก $n$ เป็นเลขจำนวนเต็มบวก แต่ก็ทำให้เกิดข้อสงสัยว่า ในเมื่อ $0!$ ไม่สามารถคำนวณมาได้จากฝั่ง $0!=0\times(-1)!$ แล้วเราจะแน่ใจได้หรือ ว่าสมการข้างต้นนี้สามารถใช้ได้ตั้งแต่ $n=1$ จริงๆ (เพราะตอนนี้เรามั่นใจแค่ว่ามันใช้ได้ตั้งแต่ $n=2$)
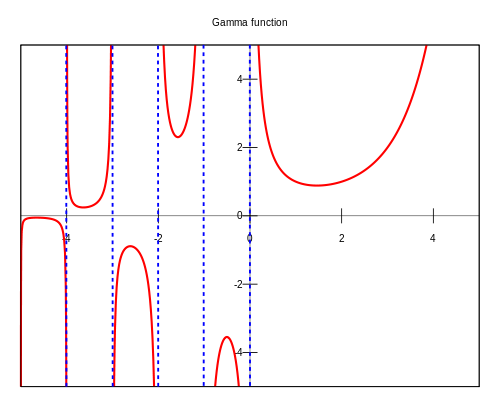
ความพยายามต่อมาคือ gamma function ที่ให้สมการอินทิเกรตยากๆ มาอันนึง (ซึ่งแก้ออกได้ด้วยการทำอินทิเกรตแยกส่วน แล้วลดรูปกลับมาให้อยู่ในรูปเดิม) สมการนี้เมื่อหาค่าทุกจุดแล้วนำมาพล็อตกราฟ จะได้ภาพการลากเส้นโค้งเชื่อมจุดต่างๆ ของ factorial นั่นเอง กราฟนี้บอกเราว่า $0!=1$ และ factorial ของจำนวนเต็มลบใดๆ หาค่าไม่ได้ ซึ่งไม่ขัดแย้งกับความพยายามก่อนหน้า
พล็อตของ gamma function – ภาพจาก Wikipedia
แม้ว่าความพยายามนี้จะเลิศเลอเพอร์เฟคแค่ไหนก็ตาม (ทั้งสมการยากๆ ที่ทำให้ดูเป็นมือโปร ทั้งการขยายขอบเขต factorial ให้ไปอยู่บนจำนวนจริงได้) แต่มันก็เกิดขึ้นหลังจากที่เรานิยามได้แล้วว่า $0!=1$ ครับ
ความพยายามสุดท้าย คือการกลับไปยังต้นกำเนิดของการที่เราอยากนิยาม factorial มาใช้เพื่อความสะดวกในการเขียนและคำนวณ นั่นก็คือเรื่องของโอกาสและความน่าจะเป็น เช่นตัวอย่างที่ว่า ถ้ามีนักเรียน 5 คน จะจัดให้ยืนเรียงต่อแถวกันได้ทั้งหมดกี่แบบ เราก็จะตอบได้ว่า คนแรกเลือกที่ยืนได้ 5 ที่ คูณกับคนที่สองเลือกยืนได้ 4 ที่ (เพราะคนแรกจองไปที่นึงแล้ว) คูณกับคนต่อมามีที่ยืนแค่ 3 ที่ (สองคนแรกจองไปสองที่) … เมื่อคิดอย่างนี้ต่อไปเรื่อยๆ เราจะเห็นได้ว่ามันย้อนกลับไปหานิยามตั้งต้นของ factorial นั่นเอง
แล้วถ้านักเรียนเหลือแค่คนเดียวหละ? เราก็จะได้ว่ามีวิธีเดียวที่จะยืน คือยืนอยู่คนเดียวให้เปล่าเปลี่ยวหัวใจเล่น ไม่มีใครมายืนนำหน้าหรือต่อแถวข้างหลัง
ส่วนที่ยากก็คือว่าถ้าไม่มีนักเรียนเหลือซักคนเลย?? คำตอบนี้อาจดูแปลก เพราะมันคือการลอกคำตอบข้างบนมาตอบในทำนองเดียวกันว่ามีวิธีเดียวที่จะยืน คือไม่ต้องมีนักเรียนยืนเลยซักคนนั่นเอง
ความพยายามนี้แม้แลดูเป็นปรัชญาอันสูงส่งเข้าใจยาก (ที่พยายามบอกเป็นนัยเชิงปฏิทรรศน์ว่า ความว่างเปล่าแท้จริงแล้วก็ยังไม่ว่าง) มันนับว่าเป็นการอธิบายที่ถูกต้องตรงจุดที่สุดในบรรดาความพยายามอธิบายที่ผ่านๆ มาเลยทีเดียว
ส่วนเรื่องจริงนั้นก็อย่างที่บอกแต่แรกสุดแล้ว ว่า $0!=1$ มันเป็นนิยามนั่นแหละ
เหตุผลก็ไม่พิศดารอะไรเลย แค่การนิยามแบบนี้แล้วจะทำให้เขียนสมการง่ายขึ้นเท่านั้น ลองคิดดูว่าถ้าเราไม่นิยามแบบนี้จะเกิดอะไรขึ้น
-
สัมประสิทธิ์ทวินาม หรือที่หลายๆ คนคุ้นเคยในรูปของ สามเหลี่ยมปัสกาลมากกว่า มันมีสูตรว่า
\[\left( x+y \right)^n = \sum\limits_{k=0}^{n} \binom{n}{k} x^{n-k}y^k\]ซึ่งถ้าไม่ได้นิยาม factorial ตามข้างต้น ก็ต้องเปลี่ยนสูตรนี้ใหม่เป็น
\[\left( x+y \right)^n = x^k + \left( \sum\limits_{k=1}^{n-1} \binom{n}{k} x^{n-k}y^k \right) + y^k\] - นิยาม permutation กับ combination ต้องกลับไปเขียนข้อยกเว้นไว้ที่
- $\binom{n}{0}$ (เลือกของ $0$ ชิ้นจากของ $n$ ชิ้นได้กี่วิธี) ซึ่งก็ยังเข้าใจได้เพราะการไม่เลือกของซักชิ้นเลยอาจเป็นข้อถกเถียง
- $\binom{n}{n}$ (เลือกของ $n$ ชิ้นจากของ $n$ ชิ้นได้กี่วิธี) อันนี้เริ่มแปลกๆ แล้ว ทำไมเลือกของทุกชิ้นต้องมีข้อยกเว้นด้วยหละ?
-
การหาค่า $e$ จากการกระจายเทย์เลอร์ จากเดิมที่เราสามารถสรุปสั้นๆ อย่างสวยงามได้ว่ามันคือ
\[e = \sum\limits_{k=0}^{\infty} \frac{1}{k!}\]ก็จะกลายเป็นสมการหน้าเกลียดๆ ที่ไม่สามารถอธิบายได้ว่าเลข $1$ ตัวแรกนั้นโผล่มาจากไหน/โผล่มาทำไม เช่นนี้
\[e = 1 + \left( \sum\limits_{k=1}^{\infty} \frac{1}{k!} \right)\]
เพราะคณิตศาสตร์คือความสวยงามครับ :)

author