ปัญหาทางการคำนวณหลายปัญหามีความยากขั้น NP ซึ่งหมายความว่าเราไม่สามารถหาอัลกอริทึมที่เร็วพอเพื่อแก้ปัญหาเหล่านั้นได้ ทางออกหนึ่งก็คือเลิกคิดถึงอัลกอริทึมเพื่อหาคำตอบที่ดีที่สุด แล้วเปลี่ยนไปคิดอัลกอริทึมที่ไม่ช้าจนเกินไปแม้จะได้คำตอบเป็นค่าประมาณก็ตาม

ถ้าเราพิสูจน์ได้ว่าอัลกอริทึมแบบประมาณนั้น ให้ที่คำตอบไม่แย่ไปกว่า 2 เท่าของคำตอบที่ดีที่สุด (สำหรับทุกๆ ความเป็นไปได้ของข้อมูลนำเข้า) อัลกอริทึมดังกล่าวจะเป็นแบบ 2-approximation สังเกตว่าเลข 2 นี่เป็นค่าคงที่และไม่ขึ้นกับขนาดของข้อมูลนำเข้า

แต่ก็ยังมีอัลกอริทึมประมาณอีกประเภท ที่ไม่สามารถประมาณคำตอบเป็นค่าคงที่ของคำตอบที่ดีที่สุด บทความนี้จะใช้ปัญหาการปกคลุมเซตเป็นตัวอย่าง

ปัญหาการปกคลุมเซต (set cover problem) ให้ข้อมูลนำเข้าเป็นเซต $S$ ซึ่งมีสมาชิกจำนวน $m$ ตัว โดยสมาชิกแต่ละตัวเป็นเซต (เรียกเซตเหล่านั้นว่า $s_1$, $s_2$, ไปจนถึง $s_m$) และเรียกยูเนียนของ $S$ ว่ายูนิเวอร์ส $U=\bigcup S$ (และเพื่อความสะดวก ให้ $n=\left|U\right|$) คำถามคือให้หา $S^{\ast }$ ซึ่งเป็นซับเซตของ $S$ โดยที่ $S^{\ast }$ มีขนาดเล็กที่สุดที่ยูเนียนของมันยังได้ผลลัพธ์เป็นยูนิเวอร์ส $U=\bigcup S^{\ast }$ อยู่

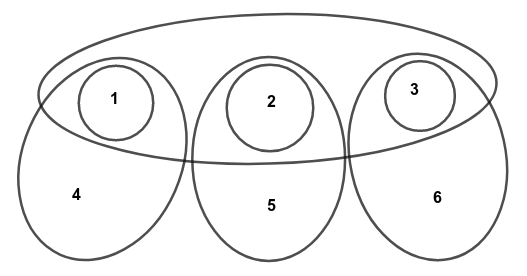
ตัวอย่างเช่น $S=\{\{1,2,3\},\{1,4\},\{2,5\},\{3,6\},\{1\},\{2\},\{3\}\}$ จะเห็นว่า $U=\{1,2,3,4,5,6\}$ และคำตอบ (ที่ดีที่สุด) ของปัญหานี้คือ $S^{\ast }=\{\{1,4\},\{2,5\},\{3,6\}\}$ ซึ่งมีขนาดคำตอบเท่ากับ 3 เซต

แผนภาพออยเลอร์ของเซตตัวอย่างข้างต้น

อัลกอริทึมประมาณค่าที่ทำงานแบบละโมบ จะเลือกหยิบ $s_x\in S$ ที่ลดจำนวนสมาชิกใน $U$ ได้มากที่สุดมาใส่ในคำตอบ $S^{\ast }$ แล้วคำนวณ $U^{\prime }=U\setminus s_x$ และ $S^{\prime }=\{s\in S:s\ne s_x\}$ ถึงตอนนี้ถ้ายูนิเวอร์ส $U^{\prime }$ ยังไม่เป็นเซตว่าง ก็จะวนกลับไปทำงานตามข้างต้นซ้ำเรื่อยๆ (โดยให้ $U\leftarrow U^{\prime }$ และ $S\leftarrow S^{\prime }$) จนกว่ายูนิเวอร์สจะกลายเป็นเซตว่างนั่นเอง

จากตัวอย่างข้างต้นแต่เปลี่ยนมาใช้อัลกอริทึมแบบละโมบ จะได้ว่ารอบแรกเราเลือกหยิบ $\{1,2,3\}$ เพราะเซตนี้ลดขนาดของยูนิเวอร์สได้มากที่สุด แล้วอีก 3 รอบต่อมาเราจะหยิบ $\{1,4\},\{2,5\},\{3,6\}$ (ในลำดับใดก็ได้) ถึงตอนนี้เราก็จะได้คำตอบแบบประมาณของคำถามนี้เรียบร้อย โดยขนาดของคำตอบแบบประมาณนี้คือ 4 เซต ดังนั้นสัดส่วนการประมาณจึงเป็น 4/3 เท่าของคำตอบที่ดีที่สุด

แล้วคำตอบแบบประมาณที่ได้จากอัลกอริทึมนี้ต่อข้อมูลนำเข้าใดๆ มีสัดส่วนเป็นเท่าไหร่หละ? หากลองสร้างตัวอย่างอื่นมาดูเรื่อยๆ จะพบว่าค่าประมาณนั้นไม่ได้เป็นจำนวนเท่าแบบค่าคงที่เลย

วิธีหาสัดส่วนค่าประมาณของอัลกอริทึมนี้ เริ่มด้วยการสมมติก่อนว่าคำตอบที่ดีที่สุดมีขนาดเป็น $k$ เซต เนื่องจากอัลกอริทึมเป็นแบบละโมบ ดังนั้นรอบแรกของอัลกอริทึม เซต $s_x$ ที่ถูกเลือกจะต้องมีขนาดอย่างน้อย $n(\frac{1}{k})$ ทำให้ยูนิเวอร์ส $U^{\prime }$ มีขนาดเหลือได้อย่างมาก $n(1-\frac{1}{k})$

ในรอบที่สอง เซตที่ถูกเลือกจะมีขนาดอย่างน้อย $n(1-\frac{1}{k})(\frac{1}{k})$ และจะทำให้ยูนิเวอร์สมีขนาดลดลงเหลืออย่างมาก $n(1-\frac{1}{k})-n(1-\frac{1}{k})(\frac{1}{k})=n(1-\frac{1}{k}{)}^2$

หลังจากอัลกอริทึมทำงานไป $i$ รอบ ขนาดของยูนิเวอร์สจะเหลืออย่างมาก $n(1-\frac{1}{k}{)}^i$ สนใจรอบที่ $i=k\ln n$ จะเห็นว่ายูนิเวอร์สมีขนาดเหลืออย่างมากแค่ $n(1-\frac{1}{k}{)}^{k\ln n}<n(\frac{1}{e}{)}^{\ln n}=1$

นั่นหมายความว่าอัลกอริทึมแบบละโมบจะทำงานอย่างมากสุดแค่ $k\ln n$ รอบ และเพราะแต่ละรอบ $S^{\ast }$ จะมีสามชิกเพิ่มขึ้นหนึ่งตัว ดังนั้นเซตคำตอบจะมีขนาดใหญ่สุดเป็น $k\ln n$ หรือเรียกได้ว่าอัลกอริทึมนี้เป็นแบบ $O(\log n)$-approximation นั่นเอง

neizod

author