อุปนัยสองชั้นกับ $(\binom{n}{r})$

Sunday, September 30, 2018, 11:17 PM

ตอนเรียนเรื่องการนับและการจัดหมู่ครั้งแรก เห็นนิยาม $n!$ กับ $n! / r!$ แล้วก็ไม่ได้ตะหงิดติดใจอะไร แต่พอมาถึง $(\binom{n}{r}) = n! / r! (n - r)!$ แล้วแอบคาใจแปลกๆ ว่าทำไมตัวเลขตัวนี้ถึงเป็นจำนวนเต็มได้ … แน่นอนหละว่ามันเป็นการนับ ยังไงซะเราคงไม่นับสิ่งที่สนใจด้วยเลขที่ไม่ใช่จำนวนเต็มเป็นแน่ แต่มันจะมีวิธีการพิสูจน์แบบอื่นที่อธิบายได้รัดกุม ขจัดปัดเป่าข้อข้องใจนี้ทิ้งไป ไม่ชวนให้กลับมาสงสัยซ้ำๆ ในอนาคตมั้ย?

ผ่านมาน่าจะเกินสิบปี จู่ๆ ก็นึกวิธีพิสูจน์ที่ฟังดูเข้าท่า (อย่างน้อยก็กับตัวเอง) ที่ทำได้ผ่านการอุปนัยสองชั้น (double induction) ออก ซึ่งนี่เป็นท่าที่เจ๋งดีเวลาต้องการพิสูจน์บนตัวแปรหลายตัว

แต่ก่อนอื่น จะขอแนะนำสัญลักษณ์ที่ใช้งานได้สะดวกในเรื่องการนับ นั่นคือแฟคทอเรียลขาขึ้น $x^{\overset{―}{n}}$ โดยหลักการทำงานของมันก็คล้ายกับแฟคทอเรียลธรรมดาที่คูณจำนวนนับที่อยู่ติดกันขึ้นไปเรื่อยๆ เป็นจำนวน $n$ ตัวนั่นแหละ เพียงแต่ว่าเลขตัวแรกในผลคูณมันไม่จำเป็นต้องเริ่มที่หนึ่งเท่านั้น แต่สามารถเริ่มที่จำนวนเต็มบวก $x$ ใดๆ ก็ได้ ซึ่งก็คือ

x^{\overset{―}{n}} = \prod_{i = 0}^{n - 1} (x + i) = x (x + 1) (x + 2) \dots (x + n - 1)

นั่นก็คือ $1^{\overset{―}{n}} = n!$ โดยมีข้อสังเกตสำคัญคือ เมื่อ $n = 0$ เราจะได้ผลคูณว่าง ซึ่งมันควรจะมีค่าเป็นเอกลักษณ์การคูณนั่นเอง

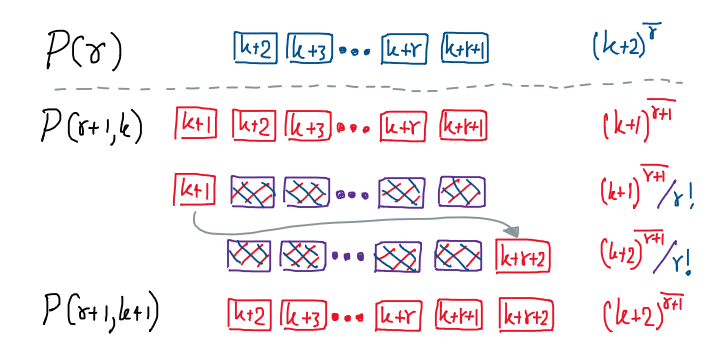
โครงร่างอย่างสังเขปสำหรับการพิสูจน์ด้วยอุปนัยสองชั้นในโจทย์ข้อนี้

กลับมาสนใจปัญหาหลักที่เราต้องการพิสูจน์ว่า $(\binom{n}{r})$ เป็นจำนวนนับ ให้ $n = r + k$ โดยที่ $r, k \in N$ ดังนั้น

(\binom{n}{r}) = (\binom{r + k}{r}) = \frac{(k + 1)^{\overset{―}{r}}}{r!}

หรือก็คือเราสามารถเปลี่ยนปัญหาดังกล่าวไปเป็นปัญหาที่ทัดเทียมกันได้ว่า “ $r!$ หารลงตัว¹กับผลคูณของจำนวนธรรมชาติที่เขียนติดกัน $r$ ตัว” นั่นก็คือเราต้องการพิสูจน์ว่า

\forall r \forall k [r! | (k + 1)^{\overset{―}{r}}]

ดังนั้น การอุปนัยชั้นแรกบน $r$ ก็คือ

P (r) : \forall k [r! | (k + 1)^{\overset{―}{r}}]

ซึ่งเราย่อมเห็นได้ทันทีว่า $P (0)$ จริงแน่นอน ด้วยสมมติฐานของการอุปนัย เราจะสมมติให้ $P (r)$ จริง เพื่อที่จะพิสูจน์ว่า $P (r + 1)$ นั้นก็ต้องจริงด้วย

ถึงตอนนี้ เราจะทำการอุปนัยซ้อนลงไปอีกชั้นบน $k$ ดังนี้

P (r, k) : r! | (k + 1)^{\overset{―}{r}}

เราก็จะเห็นอีกว่า $P (r + 1, 0)$ นั้นจริง (เพราะด้านขวาของการหารลงตัวก็คือนิยามของแฟคทอเรียลเลย) ทำให้เราตั้งสมมติฐานว่า $P (r + 1, k)$ จริงเพื่อพิสูจน์ $P (r + 1, k + 1)$ ต่อไป

ความเจ๋งของการอุปนัยสองชั้นนี้ก็คือ ตอนที่เราตั้งสมมติฐานชั้นนอกว่า $P (r)$ จริงนั้น เราจะได้ว่าสมมติฐานชั้นใน $P (r, ℓ)$ ก็จะเป็นจริงไปหมดสำหรับทุกค่า $ℓ$ ทันทีเลย (ทั้งที่เรายังพิสูจน์ชั้นในไม่เสร็จ!)² เราจะใช้งานสมมติฐานชั้นนอก $P (r)$ ที่เลือกค่าชั้นในเป็น $ℓ = k + 1$ ดังนั้น

r! | (k + 2)^{\overset{―}{r}}

เพื่อความสะดวก ให้ $s \in N$ เป็นผลหารจากการหารลงตัวดังกล่าว นั่นคือ $s r! = (k + 2)^{\overset{―}{r}}$

ถึงตรงนี้เราจะย้อนกลับมาดูสมมติฐานชั้นใน $P (r + 1, k)$ ที่บอกว่า

\begin{aligned} (r + 1)! & | (k + 1)^{\overset{―}{r + 1}} \\ | (k + 1) (k + 2)^{\overset{―}{r}} \\ (1) & | (k + 1) s r! \end{aligned}

เนื่องจากจำนวนนับใดๆ หารพหุคูณของตัวมันเองลงตัว เลือกพหุคูณเป็น $s$ บนตัวหาร $(r + 1)!$ หรือก็คือ

(r + 1)! | s (r + 1)! ⟺ (r + 1)! | (r + 1) s r!

เพราะ $(r + 1)!$ หาร $(k + 1) s r!$ และ $(r + 1) s r!$ ลงตัวทั้งคู่ ดังนั้นเราไล่ $(1)$ ต่อได้ว่า

\begin{aligned} (r + 1)! & | (k + 1) s r! + (r + 1) s r! \\ | (k + 1 + r + 1) s r! \\ | (k + 2 + r) (k + 2)^{\overset{―}{r}} \\ | (k + 2)^{\overset{―}{r + 1}} \end{aligned}

ทำให้เราสรุปได้ว่า $P (r + 1, k + 1)$ จะเป็นจริงด้วยนั่นเอง ซ.ต.พ.

คิดบทพิสูจน์ซะซับซ้อนยืดยาว เพื่อที่จะไปเห็นว่าคนอื่นใช้อัตลักษณ์

(\binom{n}{r}) = (\binom{n - 1}{r - 1}) + (\binom{n - 1}{r})

มาพิสูจน์แบบอุปนัยธรรมดาๆ ก็ออกแล้ว 😂

สัญลักษณ์การหารลงตัวนั้นให้ผลลัพธ์เป็นค่าความจริง/เท็จ (ในทำนองเดียวกับเครื่องหมายเท่ากับ) นอกจากนี้เรายังเขียนสลับฝั่งไม่เหมือนการหารเพื่อหาผลลัพธ์เชิงตัวเลขอีกด้วย พูดอีกอย่างก็คือ สัญลักษณ์ $a | b$ จะมองว่า $a$ นั้นเป็นตัวประกอบของ $b$ ↩
สำหรับเด็กคอมฯ อาจลองนึกถึงกำหนดการพลวัตรที่เราไล่ถมตารางสองมิติทีละแถวเอาก็ได้ ↩