IOI 2020: นับเห็ดเปลี่ยนชนิด

Sunday, October 25, 2020, 09:31 PM

โจทย์ข้อที่ยากทีสุดในการแข่งขัน IOI 2020 คงหนีไม่พ้นข้อที่ 2 ในวันที่ 2 ที่มีผู้เข้าแข่งขันเพียงคนเดียวที่ได้ 100 คะแนนเต็ม ตัวโจทย์เป็นแนวโต้ตอบ โดยจะให้คะแนนตามจำนวนครั้งที่โต้ตอบ ยิ่งสามารถทำได้ในจำนวนครั้งที่น้อยลงเท่าไหร่ ก็จะยิ่งได้คะแนนที่มากขึ้นเท่านั้น

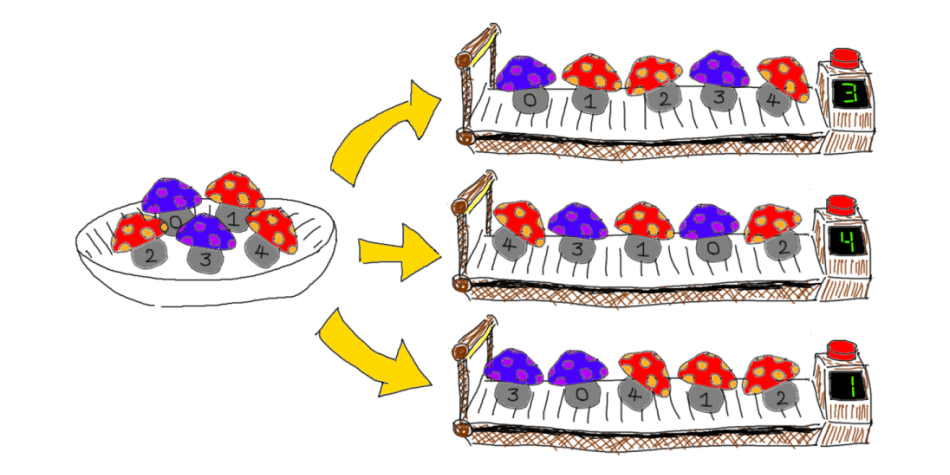
โดยเนื้อหาโจทย์อย่างสรุปเล่าได้ว่า มีเห็ดอยู่สองชนิดที่มนุษย์ไม่สามารถแยกออกได้ด้วยตนเอง ส่วนเครื่องจักรที่มีก็สามารถนับจำนวนการเปลี่ยนแปลงของชนิดเห็ดที่ใส่เข้าไปเป็นลำดับได้เท่านั้น เช่น เมื่อใส่เห็ด 5 ดอกที่มีชนิด $A B B A B$ เข้าไปตามลำดับจนเสร็จแล้วเดินเครื่อง เครื่องจักรจะตอบว่าเกิดการเปลี่ยนแปลงขึ้น 3 ครั้งนั่นเอง อย่างไรก็ตามการเดินเครื่องจักรแต่ละครั้งจะใช้พลังงานเท่ากับจำนวนเห็ดที่ใส่เข้าไป หากเรามีพลังงานอยู่ $100, 000$ หน่วยพร้อมกับเห็ดอีก $20, 000$ ดอก ซึ่งเราทราบว่าเห็ดดอกแรกสุดนั้นคือเห็ดตัวอย่างของชนิด $A$ และเราสามารถเรียงลำดับเห็ดใส่เข้าไปในเครื่องจักรอย่างไรก็ได้ จงเขียนโปรแกรมที่นับจำนวนเห็ดชนิด $A$ โดยพยายามลดจำนวนการเดินเครื่องให้เหลือน้อยที่สุดและยังใช้พลังงานไม่เกินที่กำหนด ดูเว็บที่เก็บโจทย์ต้นฉบับ

ตัวอย่างการใส่เห็ดแบบต่างๆ และคำตอบจากเครื่องจักรที่บอกจำนวนครั้งที่เห็ดเปลี่ยนชนิด

คว้าคะแนนขั้นต่ำจากข้อสังเกตพื้นฐาน

เกณฑ์การให้คะแนนขั้นต่ำสุดที่ 10 คะแนน ยินยอมให้มีการเดินเครื่องจักรได้มากถึง $20, 000$ ครั้ง ดังนั้นในแต่ละครั้งเราจะใส่เห็ดเพียง 2 ดอก โดยหนึ่งในนั้นให้เป็นเห็ดดอกแรกที่เรารู้แน่นอนว่าคือชนิด $A$ แล้วจับคู่ทีละคู่กับเห็ดดอกอื่นๆ ที่เหลือ เมื่อนับจำนวนครั้งที่ไม่มีการเปลี่ยนแปลงแล้วบวกเพิ่มอีกหนึ่งก็จะได้จำนวนของเห็ดชนิด $A$ ทั้งหมดนั่นเอง

ส่วนเกณฑ์ 25 คะแนนในบันไดขั้นถัดไปนั้น จะห้ามเดินเครื่องจักรเกิน $10, 010$ ครั้ง ซึ่งสามารถทำได้โดยใช้แนวคิดคล้ายกับข้างต้นเลย เพียงแต่ว่าเราจะใส่เห็ดเพิ่มเข้าไปเป็นครั้งละ 3 ดอกแทน โดยต้องใส่เห็ดชนิด $A$ ไว้ตรงกลางระหว่างเห็ดอีกสองดอกที่เราไม่รู้เท่านั้น เมื่อเดินเครื่องจักรแล้วจะพบว่า

ตอบ 0: เห็ดทั้ง 3 ดอกเป็นชนิด $A$
ตอบ 1: มีเห็ดชนิด $A$ อยู่ 2 ดอก และเห็ดชนิด $B$ อีก 1 ดอก (ไม่สนใจว่า $B$ คือดอกไหน)
ตอบ 2: เฉพาะเห็ดตรงกลางเป็นชนิด $A$ ส่วนอีก 2 ดอกเป็นเห็ดชนิด $B$

วางโครงร่างเทคนิคชิงคะแนนที่มากขึ้น

สำหรับเกณฑ์การให้คะแนนขั้นถัดไปจะเกิดขึ้นเมื่อสามารถเดินเครื่องจักรได้ไม่เกิน $904$ ครั้ง โดยจะคิดคะแนนเป็นสัดส่วนกับจำนวนครั้งที่เดินเครื่องจักร คือจะได้คะแนน $100 \times 226 / Q$ คะแนนเมื่อ $Q$ คือจำนวนครั้งที่เดินเครื่องนั่นเอง (คะแนนสูงสุดตัดที่ 100 คะแนน หรือก็คือได้คะแนนเต็มเมื่อเดินเครื่องไม่เกิน $226$ ครั้ง)

เทคนิคสำคัญสำหรับการคว้าคะแนนในช่วงนี้จะอาศัยข้อสังเกตจากวิธีพื้นฐานที่ผ่านมา โดยใช้เห็ดที่เรารู้ชนิดอยู่แล้วเป็นจำนวนมากมาวางสับหว่างกับเห็ดที่เราต้องการนับ ซึ่งก็คือ สมมติว่าเรามีเห็ดที่รู้แน่ๆ ว่าเป็นชนิด $A$ อยู่ $m$ ดอก เราจะจัดเห็ดใส่ถาดเป็นลำดับเช่นนี้ก่อนส่งเข้าไปให้เครื่องจักรนับจำนวนครั้งของการเปลี่ยนแปลง

\underset{2 m mushrooms}{\underset{⏟}{x_{1} A x_{2} A x_{3} A \dots x_{m} A}}

เมื่อ $x_{i}$ สำหรับ $1 \leq i \leq m$ แทนเห็ดดอกที่เรายังไม่ทราบชนิด เนื่องจากเราแค่ต้องการนับว่าจาก $x_{1}$ ถึง $x_{m}$ มีเห็ดชนิด $A$ ทั้งหมดกี่ดอก โดยจำเป็นไม่ต้องสนใจว่าแต่ละ $x_{i}$ จะเป็นเห็ดชนิดใด สังเกตว่านอกจากที่ $x_{1}$ แล้ว หาก $x_{i}$ ดอกอื่นๆ เป็นเห็ดชนิด $B$ เครื่องจักรจะนับการเปลี่ยนแปลง ณ เห็ดดอกนั้นเพิ่มได้ 2 ครั้ง ส่วนเฉพาะที่ $x_{1}$ จะนับเพิ่มเพียง 1 ครั้ง ดังนั้นหากให้คำตอบที่ได้จากเครื่องจักรคือ $R$ เราจะได้ว่า

\begin{aligned} {COUNT}_{B} (m, R) & = ⌈ \frac{R}{2} ⌉ \\ {COUNT}_{A} (m, R) & = m - {COUNT}_{B} (m, R) \end{aligned}

เทคนิคนี้ทำให้เราสามารถนับชนิดเห็ดจำนวนมากได้โดยไม่ต้องถามเครื่องจักรหลายครั้ง เช่น แม้ในกรณีที่ $n = 20, 000$ แต่หากในจำนวนนั้นเรารู้เห็ดชนิดเดียวกันเป็นจำนวน $m = 100$ อยู่ก่อนแล้ว เราสามารถใช้เครื่องจักรเพียงอีกแค่ $\frac{n - m}{m} = 199$ ครั้งเท่านั้น ก็จะนับจำนวนเห็ดแยกตามชนิดได้จนหมดครบทุกดอก

อย่างไรก็ตาม เรายังสามารถทำได้ดีกว่านั้นขึ้นไปอีก สังเกตว่าเห็ดดอกที่ $x_{1}$ นั้นถูกนับอย่างแปลกประหลาดไม่เหมือนเพื่อน ซึ่งก็คือหากคำตอบ $R$ เป็นเลขคู่ นั่นหมายความว่า $x_{1}$ ต้องเป็นเห็ดชนิด $A$ อย่างแน่นอน ดังนั้นหากในครั้งก่อนเราโชคดีเจอเห็ดชนิด $A$ ครั้งถัดไปเราก็จะสามารถจัดถาดด้วยเห็ดที่ไม่รู้ชนิดได้มากขึ้นเป็น $m + 1$ ดอก และยิ่งเราเจอเห็ดชนิด $A$ มากขึ้นเรื่อยๆ เท่าไหร่ เราก็จะยิ่งใช้เครื่องจักรได้อย่างมีประสิทธิภาพมากขึ้นเท่านั้น

แล้วเราจะโชคร้ายได้แค่ไหนกัน? หากเราไม่เจอเห็ดชนิด $A$ เลย ถึงจุดหนึ่งเห็ดชนิด $B$ จะมีจำนวนมากกว่าเห็ดชนิด $A$ เราก็จะสลับไปใช้เห็ดชนิด $B$ เป็นหลักในการสับหว่างถามเครื่องจักรแทนนั่นเอง พิจารณากรณีเริ่มต้นที่เรามีเห็ดชนิด $A$ กับ $B$ อยู่อย่างละประมาณ $m$ ดอกพอกัน หากใช้เทคนิคในแนวเดียวกับการวิเคราะห์แบบถัวเฉลี่ย (amortized analysis) จะเห็นว่าเมื่อใช้เครื่องจักรไปเรื่อยๆ ขอบเขตล่างของเห็ดกองที่ใหญ่กว่าจะมีเห็ดเพิ่มขึ้นมาหนึ่งดอกต่อการใช้เครื่องจักรสองครั้ง นั่นหมายความว่าอย่างแย่ที่สุดแล้ว เราจะถามเครื่องจักรด้วยจำนวนครั้งที่น้อยลงเหลือประมาณ

\begin{aligned} n - 2 m & = \overset{for simplicity, suppose we use the machine 2 q times}{\overset{⏞}{m + m + (m + 1) + (m + 1) + (m + 2) + (m + 2) + \dots + (m + q - 1)}} \\ = 2 (m + (m + 1) + (m + 2) + \dots + (m + q - 1)) \\ = 2 (q m + 1 + 2 + \dots + (q - 1)) \\ = 2 (q m + \frac{(q - 1) q}{2}) \\ = 2 q m + (q - 1) q \\ 0 & = q^{2} + (2 m - 1) q - (2 m - n) \\ 2 q & = 1 - 2 m \pm \sqrt{4 m^{2} - 12 m + 4 n + 1} \end{aligned}

ซึ่งก็คือ ที่ $n = 20, 000$ และ $m = 100$ จะได้ว่าต้องถามเครื่องจักรอย่างมากที่สุด $2 q \approx 145.7$ ครั้งเท่านั้น

คำถามตอนนี้จะเหลือเพียงแค่ว่า ก่อนที่จะใช้ขั้นตอนวิธีที่เล่ามาเพื่อนับเห็ดแยกชนิดในระยะที่สอง เราควรทำอย่างไรเพื่อหาเห็ดชนิดเดียวกันมาให้ได้ $m$ ดอกในระยะที่หนึ่ง หากเราใช้วิธีพื้นฐานที่สุด (10 คะแนน) ที่ค่อยๆ ถามเห็ดที่ยังไม่รู้ชนิดครั้งละดอก จะเห็นว่าเราต้องถามอย่างมากสุด $2 m - 1$ ครั้งถึงจะมั่นใจได้ว่าได้เห็ดชนิดใดชนิดหนึ่งอย่างน้อย $m$ ดอก เมื่อนำขั้นตอนย่อยในระยะที่หนึ่งกับระยะที่สองมารวมกันก็จะได้ขั้นตอนวิธีสำหรับนับเห็ดทั้งหมด อย่างไรก็ตามเราจะพบว่าขั้นตอนวิธีนี้ยังมีประสิทธิภาพไม่ดีพอ เพราะด้วยกรณีที่ผ่านมาเราอาจยังต้องถามมากถึง $199 + 146 = 345$ ครั้ง หรือคิดออกมาเป็นคะแนนได้ $100 \times 226 / 345 \approx 77$ คะแนน

เก็บงานให้เรียบร้อยมุ่งสู่คะแนนเต็ม

จากหัวข้อที่ผ่านมา จะเห็นว่าการหาเห็ดชนิดเดียวกันให้ได้ $m$ ดอกในระยะที่หนึ่งนั้นยังมีประสิทธิภาพไม่ดีนัก เราจะปรับปรุงส่วนนี้ด้วยการใช้เครื่องจักรเพียง 1 ครั้งแล้วพยายามบอกชนิดของเห็ดให้ได้ 2.5 ดอกโดยเฉลี่ย

เนื่องจากเริ่มต้นมาเรารู้ชนิดเห็ดที่แน่ชัดอยู่เพียงแค่ดอกเดียว ดังนั้นการถามครั้งแรกๆ คงเลี่ยงไม่ได้ที่ต้องถามเห็ดครั้งละหนึ่งดอก (จัดถาดเห็ดอยู่ในรูป $x_{1} A$ ) เราจะใช้เทคนิคถามหนึ่งรู้หนึ่งไม่เกิน 2 ครั้ง เพื่อรับประกันว่าจะมีเห็ดชนิดใดชนิดหนึ่งจำนวน 2 ดอก

เมื่อมีเห็ดชนิดเดียวกัน 2 ดอกแล้ว (ต่อไปนี้เพื่อความสะดวกจะสมมติให้เห็ดชนิดที่มีมากกว่าเป็นชนิด $A$ ไปเลย) เราจะจัดถาดเห็ดถามในรูป $x_{1} A x_{2} A$ ซึ่งก็คือถามครั้งเดียวระบุชนิดเห็ดได้ถึงสองดอก เพราะคำตอบในเลขฐานสองของการถามเช่นนี้จะสามารถบอกได้ทันทีว่าเห็ดดอกใดเป็นชนิดไหน ซึ่งก็คือ

บิตที่ 0 ของคำตอบเป็น 0 เมื่อและก็ต่อเมื่อ $x_{1}$ เป็นเห็ดชนิด $A$
บิตที่ 1 ของคำตอบเป็น 0 เมื่อและก็ต่อเมื่อ $x_{2}$ เป็นเห็ดชนิด $A$

เราจะใช้เทคนิคถามสองรู้สองอีกเพียงไม่เกิน 2 ครั้ง ก็จะได้เห็ดชนิด $A$ มาอย่างน้อย 3 ดอก

หลังจากนั้นเราจะจัดถาดด้วยเห็ดที่ไม่รู้ชนิดครั้งละสามดอกเช่นนี้ $x_{1} A x_{2} A x_{3} A$ จากเทคนิคที่เคยเห็นผ่านมาแล้ว เราคงบอกได้ไม่ยากว่า $x_{1}$ คือเห็ดชนิด $A$ หรือไม่ อย่างไรก็ตามสำหรับ $x_{2}$ และ $x_{3}$ นั้น เราพบว่า

หากคำตอบเป็น 0 หรือ 1 นั่นคือ $x_{2}$ และ $x_{3}$ เป็นเห็ดชนิด $A$ ทั้งคู่
หากคำตอบเป็น 4 หรือ 5 นั่นคือ $x_{2}$ และ $x_{3}$ เป็นเห็ดชนิด $B$ ทั้งคู่
หากคำตอบเป็น 2 หรือ 3 จะบอกได้แค่ว่า $x_{2}$ กับ $x_{3}$ เป็นเห็ดชนิดต่างกัน

เทคนิคดังกล่าวคือการถามสามอาจรู้หนึ่งหรือสาม หากมันล้มเหลวโดยระบุชนิดเห็ดได้เพียงดอกเดียว อย่างน้อยเราจะรู้ว่าเห็ดอีกสองดอกต้องไม่เป็นชนิดเดียวกัน ถึงตอนนี้เราจะจัดการกับความกำกวมนี้โดยใช้เห็ดชนิด $B$ เข้ามาช่วย ซึ่งแบ่งได้เป็น 2 กรณี คือ

กรณีแรกเมื่อเรามีเห็ดชนิด $B$ อยู่น้อยกว่า 2 ดอก เราจะใช้เทคนิคแบบเดียวกับถามสองรู้สองเลย เพียงแต่เปลี่ยนไปจัดถาดเห็ดด้วย $x_{3} A x_{4} A$ นอกจากนี้อย่าลืมว่าชนิดของเห็ด $x_{3}$ ที่หาได้ก็จะบ่งบอกย้อนไปถึงชนิดของเห็ด $x_{2}$ ด้วย เราจะเรียกเทคนิคนี้ว่าแก้กำกวมถามสองรู้สาม

ส่วนอีกกรณีเราจะจัดถาดเห็ด $B x_{2} B A x_{3} A x_{4} A x_{5}$ เพื่อถามเครื่องจักร เมื่อนำคำตอบที่ได้ไปลบหนึ่ง (เพราะมีการเปลี่ยนแปลงแน่ๆ จากคู่เห็ดที่เราตั้งใจใส่เข้าไปหนึ่งครั้ง) คำตอบใหม่จะมีค่าได้ตั้งแต่ 0 ถึง 7 พิจารณาคำตอบใหม่นี้ในเลขฐานสองจะพบว่า

บิตที่ 2 ของคำตอบใหม่เป็น 0 เมื่อและก็ต่อเมื่อ $x_{3}$ เป็นเห็ดชนิด $A$
บิตที่ 1 ของคำตอบใหม่เป็น 0 เมื่อและก็ต่อเมื่อ $x_{4}$ เป็นเห็ดชนิด $A$
บิตที่ 0 ของคำตอบใหม่เป็น 0 เมื่อและก็ต่อเมื่อ $x_{5}$ เป็นเห็ดชนิด $A$

เรียกกระบวนการนี้ว่าแก้กำกวมถามสี่รู้สี่ (และเช่นเคย ชนิดเห็ดของ $x_{3}$ จะบ่งบอกชนิดเห็ด $x_{2}$ ) ดังนั้นในภาพรวม เราจะใช้เทคนิคถามสามอาจรู้หนึ่งหรือสามไปเรื่อยๆ แล้วสลับไปเลือกใช้เทคนิคแก้กำกวมถามสองรู้สามหรือแก้กำกวมถามสี่รู้สี่ จนกระทั่งเราได้เห็ดชนิด $A$ มาอย่างน้อย $m$ ดอก

แล้วเราจะต้องใช้เครื่องจักรในระยะที่หนึ่งด้วยเทคนิคเหล่าไปเป็นจำนวนเท่าไหร่? สมมติว่าเราสนใจ $m$ ขนาดใหญ่ๆ เราอาจตัดการถามหนึ่งรู้หนึ่งและถามสองรู้สองที่จะเกิดขึ้นเพียงไม่กี่ครั้งออกจากการวิเคราะห์ไปเลย หลังจากนั้นเราจะถามสามอาจรู้หนึ่งหรือสามเป็นส่วนใหญ่ ซึ่งอาจให้ประสิทธิภาพแย่ได้หากต้องแก้กำกวมเป็นจำนวนมาก แต่เนื่องจากการแก้กำกวมถามสองรู้สามเกิดขึ้นได้อย่างมากที่สุดเพียง 2 ครั้ง เราอาจตัดมันออกจากการวิเคราะห์ได้ด้วยเช่นกัน เหลือเพียงแค่การแก้กำกวมถามสี่รู้สี่ ดังนั้นด้วยคู่ของการถามสามอาจรู้หนึ่งหรือสามและแก้กำกวมถามสี่รู้สี่จะระบุชนิดเห็ดได้ 5 ดอกต่อการถาม 2 ครั้ง และเนื่องจากเราอาจต้องระบุชนิดเห็ดมากถึง $2 m$ ดอก ดังนั้นเราจะต้องถามประมาณ $2 m / 2.5 = 0.8 m$ ครั้งนั่นเอง

ให้ $Q_{n} (m)$ เป็นจำนวนครั้งทั้งหมดที่ต้องถามเครื่องจักร ก็จะได้ว่า

\begin{aligned} Q_{n} (m) & = 0.8 m + 1 - 2 m \pm \sqrt{4 m^{2} - 12 m + 4 n + 1} \\ Q_{n}^{'} (m) & = \frac{4 m - 6}{\sqrt{4 m^{2} - 12 m + 4 n + 1}} - \frac{6}{5} \end{aligned}

แก้อนุพันธ์ $Q_{n}^{'} (m) = 0$ เพื่อหาค่า $m$ ที่เหมาะสมที่สุด จะได้

m = \frac{3}{4} (2 \pm \sqrt{n - 2})

นั่นก็คือ ในกรณีที่ $n = 20, 000$ เราควรหาเห็ดชนิดเดียวกันในระยะที่หนึ่งไว้ประมาณ $m \approx 107.6$ ดอก แล้วหลังจากนั้นจึงแค่นับชนิดเห็ดที่สนใจพร้อมค่อยๆ ขยายปริมาณเห็ดที่รู้ชนิดในระยะที่สอง ซึ่งทั้งหมดนี้จะทำให้เครื่องจักรถูกเรียกใช้รวมไม่เกิน $Q_{n} (108) \approx 225.5$ ครั้ง

โค้ด

#include "mushrooms.h"
#include <bits/stdc++.h>
using namespace std;

bool swapped = false;
bool conflict = false;
int i = 1;
int just_count_A = 0;
int just_count_B = 0;
vector<int> A = { 0 };
vector<int> B = { };

int calc_pivots_size(int n) {
    return 1.5 + (3*sqrt(n-2)/4);
}

void make_swap() {
    swapped = not swapped;
    swap(just_count_A, just_count_B);
    swap(A, B);
}

bool decide_swap() {
    if (A.size() < B.size()) {
        make_swap();
    }
    return true;
}

int handle_parity(int parity) {
    (parity == 0 ? A : B).push_back(i);
    return 1;
}

int handle_pair(int raw_info) {
    int flag2b = raw_info >> 1;
    if (flag2b & 0b01) {
        conflict = true;
        return 0;
    }
    (flag2b & 0b10 ? B : A).push_back(i);
    (flag2b & 0b10 ? B : A).push_back(i+1);
    return 2;
}

int handle_conflict_slow(int flag2b) {
    (flag2b & 0b01 ? A : B).push_back(i);
    (flag2b & 0b01 ? B : A).push_back(i+1);
    (flag2b & 0b10 ? B : A).push_back(i+2);
    conflict = false;
    return 3;
}

int handle_conflict_fast(int raw_info) {
    int flag3b = raw_info - 1;
    (flag3b & 0b100 ? A : B).push_back(i);
    (flag3b & 0b100 ? B : A).push_back(i+1);
    (flag3b & 0b010 ? B : A).push_back(i+2);
    (flag3b & 0b001 ? B : A).push_back(i+3);
    conflict = false;
    return 4;
}

void get_pivots(int n) {
    int info;
    int size = calc_pivots_size(n);
    while (decide_swap() and (int)A.size() < size and i+4 < n) {
        if (not conflict) {
            switch (A.size()) {
                case 1:
                    i += handle_parity(use_machine({ i, A[0] }));
                    break;
                case 2:
                    info = use_machine({ i, A[0], i+1, A[1] });
                    i += handle_parity(info%2);
                    i += handle_parity(info/2);
                    break;
                default:
                    info = use_machine({ i, A[0], i+1, A[1], i+2, A[2] });
                    i += handle_parity(info%2);
                    i += handle_pair(info);
            }
        } else if (B.size() < 2) {
            info = use_machine({ i+1, A[0], i+2, A[1] });
            i += handle_conflict_slow(info);
        } else {
            info = use_machine({ B[0], i, B[1], A[0], i+1, A[1], i+2, A[2], i+3 });
            i += handle_conflict_fast(info);
        }
    }
}

vector<int> make_sample(int size) {
    vector<int> sample = { };
    for (int j=0; j<size; j++) {
        sample.insert(sample.end(), { i+j, A[j] });
    }
    return sample;
}

void count_the_rest(int n) {
    while (decide_swap() and i < n) {
        int test_size = min((int)A.size(), n-i);
        int info = use_machine(make_sample(test_size));
        i += handle_parity(info%2);
        i += test_size-1;
        just_count_A += (test_size-1) - (info/2);
        just_count_B += info/2;
    }
}

int count_mushrooms(int n) {
    get_pivots(n);
    count_the_rest(n);
    if (swapped) {
        make_swap();
    }
    return A.size() + just_count_A;
}