ปัญหาการจ้างเลขาและค่า $1 / e$

Saturday, November 7, 2020, 09:18 AM

ลองจินตนาการว่าเรากำลังจะเปิดบริษัทแต่ยังขาดพนักงานเลขา ซึ่งตำแหน่งดังกล่าวถือว่าเป็นตำแหน่งฮอตฮิตที่บริษัทไหนๆ ก็ต่างแย่งชิงตัว การเรียกผู้สมัครมาสัมภาษณ์งานจึงจำเป็นต้องตอบรับทันทีเดี๋ยวนั้น มิเช่นนั้นแล้วก็รับประกันได้เลยว่าผู้สมัครจะถูกบริษัทอื่นแย่งตัวไปในทันทีที่เขาก้าวเท้าออกจากออฟฟิศ

สมมติว่าเราสามารถเรียกผู้สมัครมาสัมภาษณ์ได้มากที่สุด $n$ คน โดยถือว่าก่อนสัมภาษณ์เราไม่รู้อะไรเกี่ยวกับผู้สมัครเลย และเมื่อสัมภาษณ์เสร็จเราก็จะบอกได้แค่ว่าผู้สมัครคนนี้ดีกว่าหรือแย่กว่าผู้สมัครคนก่อนๆ ที่เคยสัมภาษณ์ เราจะมีเทคนิคอย่างไรในการเฟ้นหาผู้สมัครเพียงหนึ่งคนที่ดีที่สุด?

มองเผินๆ นี่อาจจะดูเหมือนปัญหาที่ไม่น่าเป็นไปได้ ในเมื่อเราไม่รู้ว่าใครดีกว่าใครจนกว่าจะได้สัมภาษณ์ แต่พอสัมภาษณ์เสร็จก็ต้องตอบรับว่าจะให้ร่วมทางกับบริษัทเราหรือไม่ซะแล้ว หากเราถอดใจไม่วางแผนใดๆ และเลือกตอบรับผู้สมัครแบบสุ่ม โอกาสที่จะได้ผู้สมัครที่ดีที่สุดก็จะมีเพียงแค่ $1 / n$ เท่านั้น

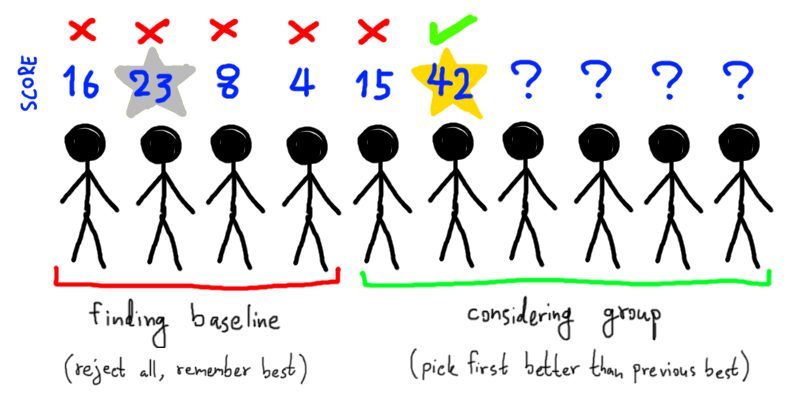
แต่เนื่องจากเราสามารถเปรียบเทียบผู้สมัครได้ หากเราลองสัมภาษณ์ผู้สมัครคนแรกดูก่อน (และต้องแข็งใจบอกปฏิเสธไป) เพื่อเป็นบรรทัดฐานว่าเราอยากได้ผู้สมัครประมาณไหน เมื่อสัมภาษณ์ต่อไปและพบว่าผู้สมัครคนที่สองดีกว่าคนแรก อย่างน้อยโอกาสที่เขาจะเป็นผู้สมัครที่ดีที่สุดก็มีมากกว่าการสุ่มแน่ๆ

หากเราแบ่งการสัมภาษณ์ออกเป็น 2 ช่วง โดยช่วงแรกสัมภาษณ์ผู้สมัครเป็นสัดส่วน $0 < r \leq 1$ ต่อผู้สมัครทั้งหมด เพื่อหาบรรทัดฐานของผู้สมัครที่เราต้องการ แล้วในช่วงหลังจึงสัมภาษณ์ผู้สมัครที่เหลือ เมื่อใดที่เจอผู้สมัครที่ดีกว่าทุกคนที่เคยเจอมา เราจะตอบรับให้ผู้สมัครคนนี้มาร่วมงานทันที โอกาสที่ผู้สมัครคนนี้จะเป็นผู้สมัครที่ดีที่สุดก็คือ

P (pick 1^{s t}) = \sum_{k = 1}^{n} P (baseline is k^{t h}) \cdot P (saw k^{t h} pick 1^{s t})

โดยที่

$1^{s t}$ คือผู้สมัครที่ดีที่สุด (อันดับหนึ่ง) $n^{t h}$ คือผู้สมัครที่แย่ที่สุด และไม่มีใครอยู่อันดับเดียวกัน
$pick 1^{s t}$ แทนเหตุการณ์ที่ได้ผู้สมัครที่ดีที่สุดจากกระบวนการทั้งหมด
$baseline is k^{t h}$ แทนเหตุการณ์ที่ผู้สมัครอันดับที่ $k^{t h}$ เป็นบรรทัดฐานในการสัมภาษณ์ช่วงแรก
$saw k^{t h} pick 1^{s t}$ แทนเหตุการณ์ที่ใช้ $k^{t h}$ เป็นฐานแล้วได้ผู้สมัครที่ดีที่สุดในการสัมภาษณ์ช่วงหลัง

ซึ่งเราจะเห็นว่า

$saw 1^{t h} pick 1^{s t}$ เป็นไปไม่ได้
$baseline is k^{t h}$ หมายความว่า ในการสัมภาษณ์ช่วงแรก นอกจากจะเห็นผู้สมัครอันดับที่ $k^{t h}$ แล้ว จะต้องไม่เห็นผู้สมัครตั้งแต่อันดับ $1^{s t}$ ถึง $(k - 1)^{t h}$ ด้วย

หาก $n$ มีขนาดเล็กเราจะต้องคำนวณแตกกรณียิบย่อยมากมาย ดังนั้นจะพิจารณาเฉพาะเมื่อ $n$ มีขนาดใหญ่ ที่เราจะเห็นว่าพจน์หลังๆ มีค่าลดลงอย่างรวดเร็ว ทำให้เราสามารถประมาณด้วยอนุกรมอนันต์ได้ ซึ่งก็คือ

\begin{aligned} P (pick 1^{s t}) & = \sum_{k = 1}^{n} P (baseline is k^{t h}) \cdot P (saw k^{t h} pick 1^{s t}) \\ \approx r \cdot 0 + r (1 - r) \cdot 1 + r {(1 - r)}^{2} \cdot \frac{1}{2} + r {(1 - r)}^{3} \cdot \frac{1}{3} + \dots \\ = r \sum_{k = 1}^{\infty} \frac{{(1 - r)}^{k}}{k} \end{aligned}

ให้ $x = (1 - r)$ ปัญหาย่อยของเราจะแปลงไปเป็นการหาผลลัพธ์ของอนุกรมฮาร์โมนิค ที่แต่ละพจน์มีผลคูณของเลขยกกำลังติดมาด้วย ดังนี้

\sum_{k = 1}^{\infty} \frac{x^{k}}{k} = x + \frac{x^{2}}{2} + \frac{x^{3}}{3} + \frac{x^{4}}{4} + \dots

ซึ่งเราสามารถใช้อนุกรมเทย์เลอร์มาช่วยแก้ได้ โดยเทคนิคคือเลือกใช้ฟังก์ชันที่อนุพันธ์อันดับ $k$ มีพจน์ $(k - 1)!$ โผล่เข้ามา เพื่อที่เราจะได้เอาไปตัดกับ $1 / k!$ จากการกระจายเทย์เลอร์ จนได้ผลลัพธ์เป็นอนุกรมในรูปฮาร์โมนิคอย่างที่เราต้องการ ซึ่งฟังก์ชันที่มีสมบัติดังกล่าวก็คือฟังก์ชันตระกูล $\log$ นั่นเอง

\begin{array}{ccc} f (x) & \log x & \log (1 - x) \\ f^{'} (x) & \frac{1}{x} & - \frac{1}{1 - x} \\ f^{″} (x) & - \frac{1}{x^{2}} & - \frac{1}{(1 - x)^{2}} \\ f^{(3)} (x) & \frac{2!}{x^{3}} & - \frac{2!}{(1 - x)^{3}} \\ f^{(4)} (x) & - \frac{3!}{x^{4}} & - \frac{3!}{(1 - x)^{4}} \\ ⋮ \\ f^{(k)} (x) & \frac{(- 1)^{k + 1} (k - 1)!}{x^{k}} & - \frac{(k - 1)!}{(1 - x)^{k}} \end{array}

เลือกกระจาย $\log (1 - x)$ รอบจุด 0 จะได้ว่า

\begin{aligned} \log (1 - x) & = \sum_{k = 1}^{\infty} \frac{f^{(k)} (0)}{k!} (x - 0)^{k} \\ = \sum_{k = 1}^{\infty} - \frac{(k - 1)!}{(1 - 0^{k}) k!} x^{k} \\ = - \sum_{k = 1}^{\infty} \frac{x^{k}}{k} \end{aligned}

ดังนั้น

P (pick 1^{s t}) \approx - r \log r

แล้วใช้เทคนิคอนุพันธ์จากแคลคูลัสเพื่อหาค่า $r$ ที่เหมาะสม

\begin{aligned} 0 & = \frac{d}{d r} (- r) \log r \\ = (- r) \frac{d}{d r} \log r + \log r \frac{d}{d r} (- r) \\ = - 1 - \log r \\ r & = \frac{1}{e} \end{aligned}

ก็จะได้คำตอบว่า สัดส่วนที่เหมาะสมที่สุดที่ควรใช้หาบรรทัดฐานในช่วงแรก คือ $1 / e \approx 36.8 %$ นั่นเอง นอกจากนี้เมื่อย้อนกลับไปคำนวณความน่าจะเป็น ก็จะเห็นว่า $P (pick 1^{s t}) \approx 1 / e$ อีกด้วย!