ความเร็วของอัลกอริทึมที่พบเห็นกันได้ทั่วไป ก็มักจะหนีไม่พ้น $O(n)$ หรือไม่ก็ $O(n \log n)$ ซึ่งนั่นเป็นความเร็วสำหรับอัลกอริทึมพื้นฐานในวิชาพวก 101 อย่างไรก็ตามอัลกอริทึมที่ซับซ้อนในชีวิตจริงอาจไม่ได้มีความเร็วที่เรียบง่ายเช่นนั้น

จุดที่น่าสนใจคืออัลกอริทึมหลายตัว (ทั้งเรียบง่ายและซับซ้อน) นั้นมักจะมีความเร็วเป็นพหุคูณของ $O(\log n)$ ติดเข้ามาด้วย ซึ่งมันมักสะท้อนมาจากการใช้เทคนิคแบ่งแยกและเอาชนะนั่นเอง

อันที่จริง ส่วนที่เป็นลอการิทึมนั้นมันอาจซับซ้อนกว่าแค่ $O(\log n)$ ก็ได้ คือสามารถเป็นอนุกรมของลอการิทึมที่ยกกำลังได้อีกด้วย เราอาจเรียกความเร็วเช่นนี้ว่ามันคือความเร็วแบบ $\mathbf{polylog}(n)$ โดยที่

\[\mathbf{polylog}(n) = a_k(\log n)^k + a_{k-1}(\log n)^{k-1} + a_{k-2}(\log n)^{k-2} + \dots + a_1(\log n) + a_0\]

สำหรับจำนวนเต็มบวก $k \in \mathbb{Z}^+$ ซึ่งเราจะเห็นได้ทันทีเลยว่าพจน์ $a_k(\log n)^k$ นั้นชนะแบบครอบงำพจน์อื่นๆ ที่เหลือทั้งหมดเมื่อ $n\to\infty$ ดังนั้นถ้าจะวิเคราะห์แบบหยาบๆ เราอาจจะสนใจหยิบแค่พจน์นี้มาเป็นตัวแทนของทั้ง $\mathbf{polylog}(n)$ ก็ย่อมได้

จุดสำคัญก็คือ $O((\log n)^k)$ นั้นเร็วกว่า $O(n^\epsilon)$ เสมอ ไม่ว่าเราจะเลือก $\epsilon \in \mathbb{R}^+$มาเล็กแค่ไหน! วิธีที่ตรงไปตรงมาที่สุดก็คือแปลงความซับซ้อนนี้ให้อยู่ในรูปของจำนวนบิตแล้วเอามาเทียบกันเลย ซึ่งก็คือ

\[\begin{align} (\log n)^k &= 2^{k \log\log n} \\ n^\epsilon &= 2^{\epsilon \log n} \end{align}\]

จะเห็นได้ทันทีว่า $(\log n)^k$ นั้นโตช้ากว่าแน่นอน เพราะ $\log\log n$ นั้นโตช้ากว่า $\log n$

แต่ถ้าใครยังเห็นไม่ชัด หรืออยากได้อีกวิธีหนึ่งที่อาจจะเข้าใจได้ง่ายกว่า (แถมยังสวยงามและมีลูกเล่นอีกด้วย) ก็คือการนำเอาแคลคูลัสเข้ามาช่วยแก้ปัญหานี้ ซึ่งก็คือเราจะเปลี่ยนไปหา $\lim_{n\to\infty} f(n)/g(n)$ แทน โดยมันมีผลลัพธ์อยู่สามแบบที่สามารถตีความออกมาได้ดังนี้

• ลู่เข้าสู่ศูนย์: พจน์ด้านบนโตช้ากว่าพจน์ด้านล่าง (ซึ่งก็คือ $O(f(n))$ นั้นโตช้ากว่า $O(g(n))$)
• ลู่เข้าหาค่าคงตัว: ทั้งสองพจน์โตด้วยความเร็วเทียบเคียงกัน
• ลู่ออกไปยังอนันต์: พจน์ด้านล่างโตช้ากว่าพจน์ด้านบน

เพราะงั้นเราก็จะมาโซ้ยสมการกันหน่อย โดยเริ่มจากให้ $f(n)=(\log n)^k$ และ $g(n) = n^\epsilon$ ทีนี้สังเกตว่าเมื่อให้ $n\to\infty$ แล้วค่า $(\log n)^k/n^\epsilon$ จะอยู่ในรูปแบบไม่กำหนด ถึงตรงนี้เราอาจนำเอากฎของ L’Hôpital มาช่วยได้ ซึ่งก็คือ

\[\begin{align} \lim_{n\to\infty} \frac{(\log n)^k}{n^\epsilon} &= \lim_{n\to\infty} \frac{\frac{d}{dn}(\log n)^k}{\frac{d}{dn}n^\epsilon} \\ &= \lim_{n\to\infty} \frac{k(\log n)^{k-1}/n}{\epsilon n^{\epsilon-1}} \\ &= \frac{k}{\epsilon} \lim_{n\to\infty} \frac{(\log n)^{k-1}}{n^\epsilon} \end{align}\]

นั่นคือเราจะได้พจน์ในลิมิตหน้าตาแบบเดิมออกมา ซึ่งถ้ามองเผินๆ ก็อาจคิดว่านี่มันติดลูปแล้วแก้ไม่ออกหนิ แต่ที่จริงแล้วสิ่งสำคัญที่เปลี่ยนไปก็คือพจน์ $(\log n)^k$ ที่ลดกำลังลงมาเป็น $(\log n)^{k-1}$ เราจึงสามารถประยุกต์ใช้เทคนิคนี้ซ้ำๆ ได้จนพจน์ดังกล่าวหายไปในที่สุด

\[\lim_{n\to\infty} \frac{(\log n)^k}{n^\epsilon} = \frac{k}{\epsilon} \lim_{n\to\infty} \frac{(\log n)^{k-1}}{n^\epsilon} = \frac{k(k-1)}{\epsilon^2} \lim_{n\to\infty} \frac{(\log n)^{k-2}}{n^\epsilon} = \cdots = \frac{k!}{\epsilon^k} \lim_{n\to\infty} \frac1{n^\epsilon}\]

ถึงตอนนี้ก็ตอบได้แล้วว่าลิมิตตัวนี้ลู่เข้าสู่ศูนย์ หรือย้อนกลับไปสรุปตั้งแต่แรกสุดได้ว่า $O(\mathbf{polylog}(n))$ นั้นเร็วกว่า $O(n^\epsilon)$ เสมอ ไม่ว่า $\epsilon$ จะมีขนาดเล็กแค่ไหนก็ตาม (แต่ต้องมากกว่าศูนย์)

พูดอย่างหยาบๆ ก็คือ $\mathbf{polylog}(n)$ นั้นเร็วมากๆ จนเกือบจะเป็นความเร็วแบบค่าคงที่เลยทีเดียว

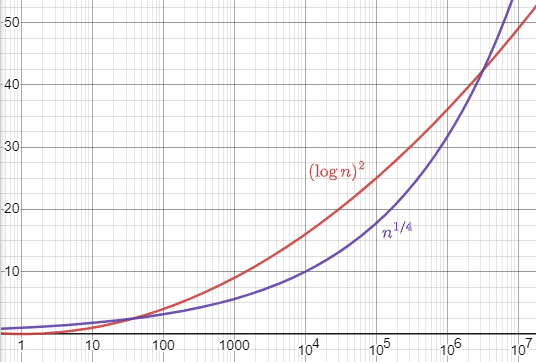
ตัวอย่างพล็อตเทียบระหว่าง $(\log n)^2$ (สีแดง) กับ $n^{1/4}$ (สีม่วง) โดยแกนนอนใช้มาตราส่วนลอการิทึม ซึ่งจะเห็นว่าเส้นสีแดงนั้นโตแบบพาราโบลา ส่วนเส้นสีม่วงเป็นการโตแบบเอกซ์โพเนนเชียล

จากข้อสังเกตข้างต้น กอปรกับความซับซ้อนของอัลกอริทึมในชีวิตจริงที่มักติดพจน์ดังกล่าวบ่อยๆ ก็ทำให้เกิดสัญลักษณ์ $\tilde{O}(f(n))$ (อ่านว่า soft-O) เพื่อเขียนย่อแทนความเร็วแบบ $O(f(n) {\cdot} \mathbf{polylog}(f(n)))$ นั่นเอง โดยบทความงานวิจัยส่วนใหญ่ที่สามารถปรับปรุงอัลกอริทึมให้เร็วเป็น $\tilde{O}(n)$ ก็มักจะเขียนจั่วหัวไว้ว่ามันคือความเร็วแบบ “เกือบเป็นเชิงเส้น” (nearly-linear time) อีกด้วย

ขอบคุณ @sorawee_p, @lbundit และ @puripant สำหรับคำแนะนำที่ทำให้บทวิเคราะห์นี้สมบูรณ์ครับ