สงสัยมานานแล้วว่า ในโลกความจริงเนี่ย ธนาคารเค้าคิดดอกเบี้ยกันยังไง อย่างเช่น “ดอกเบี้ย 100% ต่อปี” (ขอเริ่มด้วยเลขที่ไม่ตรงกับโลกจริงไปก่อน) ก็แปลว่าถ้าเราฝากเงินตั้งแต่ต้นปีไปจนจบปี เราจะได้เงินเพิ่มขึ้นมาอีกหนึ่งเท่าตัว (รวมเป็นมีเงิน 2 เท่าของเงินตั้งต้น)

เพราะงั้นคำถามแรกที่ผุดขึ้นมาอย่างเป็นธรรมชาติมากๆ ก็คือถ้าเราฝากไม่ครบทั้งปีหละ? ซึ่งตรงนี้ถ้าใครตั้งใจเรียนคณิตศาสตร์ม.ปลายมากเกินไปหน่อย (เช่นเรา 55555) ก็อาจจะสับสนกับเรื่องการคิดดอกเบี้ยแบบซอยเป็นช่วงย่อยๆ ที่สุดท้ายจะทำให้เรามีเงินเป็น 2.718 เท่าได้ (เรื่องเล่ามาตรฐานของการได้มาซึ่งค่า $e$) และอาจงงว่า “100% ต่อปี” เนี่ยมันไม่ใช่ 100% ต่อปีจริงๆ (ในเซนส์ของดอกเบี้ยไม่ทบต้น) แต่มันเป็นเลขที่ลดลงมา (เป็นเลขอะไรซักอย่าง เช่น 69.31% ต่อปี) แทนหรือเปล่า???

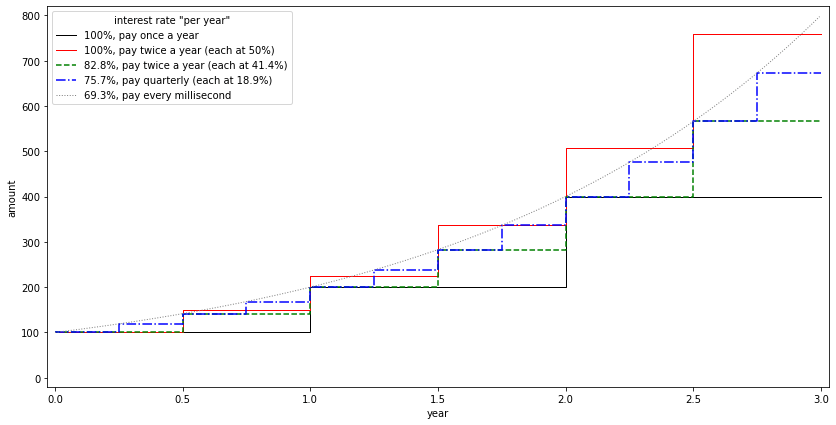
ตัวอย่างการฝากเงินเป็นระยะเวลาสามปี โดยที่แต่ละธนาคารคิดอัตราดอกเบี้ย/รอบแบ่งจ่ายไม่เท่ากัน แต่ให้ผลลัพธ์เป็นเงินฝากทบต้นที่มีค่าเท่ากันทุกต้นปี (ยกเว้นธนาคารสีแดงที่จ่ายดอกแพงกว่าธนาคารอื่นๆ)

ปรากฏว่าโลกความจริงมันคิดอะไรง่ายกว่านั้นเยอะ เพราะธนาคารเค้าไม่ได้คิดดอกเบี้ยให้ย่อยๆ ตามช่วงเวลาแล้วทบไปเรื่อยๆ แต่จะคิดโง่ๆ เลยว่าฝากเงินเป็นระยะเวลากี่วันในหนึ่งปี แล้วก็เอาไปเทียบอัตราส่วนตรงๆ เช่น ธนาคารบอกว่า “ดอกเบี้ย 100% ต่อปี คิดดอกเบี้ยตอนปลายปี” มันจะหมายความว่า สมมติเราเริ่มฝากเงินตอนปลายมีนาต้นเมษา แล้วถอนออกมาตอนปลายกันยาต้นตุลา ก็แปลว่าเราจะฝากเงินเป็นระยะเวลาประมาณ 50% ของทั้งปี เพราะงั้นเมื่อถึงตอนสิ้นปี เราก็จะได้ดอกเบี้ยเป็น 50% ของเงินตั้งต้นก้อนนี้ (แม้ว่าเราจะถอนเงินก้อนนั้นออกไปก่อนแล้วก็ตามที) การทบยอดของธนาคารจะเกิดขึ้นเมื่อธนาคารนำเงินดอกเบี้ยก้อนนั้นใส่กลับเข้ามาในบัญชีเรา ซึ่งก็คือจะเริ่มการคิดดอกเบี้ยของดอกเบี้ยก้อนนี้ได้ในปีถัดไปนั่นเอง

ทีนี้ “ความไม่ลงรอย” ระหว่างข้อมูลที่ธนาคารแจ้งกับผลลัพธ์เงินฝากในความโลกจริงเนี่ย มันจะเกิดขึ้นเมื่อธนาคาร(บางแห่ง?)ยังคงใช้กรอบของการสื่อสารว่า “ดอกเบี้ยต่อปี” อยู่ ในขณะที่หลังบ้านการทำงานจริงของธนาคารเหล่านั้นคือคิดดอกเบี้ยให้ทุกครึ่งปีแล้วเอาเข้าบัญชีให้เลย ทำให้เกิดการทบต้นในช่วงเวลาที่สั้นกว่าหนึ่งปีได้ ดังนั้น ถ้าเราฝากเงินตั้งแต่ต้นปีโดยไม่ถอนเลยกับแผน “ดอกเบี้ย 100% ต่อปี แบ่งจ่ายดอกเบี้ยเป็นสองงวด (นั่นคือแต่ละงวดจะจ่ายดอกเบี้ย 100%/2 = 50%)” แปลว่าจริงๆ แล้วเมื่อจบปีเราจะได้ดอกเบี้ยเป็น 125% ต่างหาก (ครึ่งปีแรกได้ดอกเบี้ย 50% จากเงินต้นเพียงอย่างเดียว ส่วนครึ่งปีหลังก็ยังได้ดอกเบี้ยอีก 50% เพียงแต่ว่าคราวนี้คิดจากเงินต้นบวกกับดอกเบี้ยก้อนแรกแล้ว ในทางปฎิบัติ ดอกเบี้ยก้อนหลังนี้มันจึงกลายเป็นมีสัดส่วน 75% ของเงินต้นแทนนั่นเอง)

ในภาษาธนาคาร จะเรียกนโยบายจ่ายดอกเบี้ยด้วยตัวเลขรอบปีแบบนี้ว่า APR (annual percentage rate) ซึ่งไม่ได้บอกอะไรเลยเกี่ยวกับว่ามีการจ่ายดอกเบี้ยปีละกี่รอบ และเค้าจะเรียกดอกเบี้ยจริงๆ ที่ได้รับในทางปฎิบัติ (ผ่านการแบ่งจ่าย-ทบต้นหลายรอบ) นั้นว่า EPR (effective percentage rate) ซึ่งจะเห็นได้ว่าถ้าธนาคารแบ่งจ่ายดอกเบี้ยปีละรอบ ค่า APR จะเท่ากับ EPR พอดี แต่ถ้ายิ่งแบ่งจ่ายเยอะ EPR ก็จะยิ่งเยอะกว่า APR นั่นเอง หรือเขียนเป็นความสัมพันธ์ได้ว่า

\[1 - EPR = \left( 1 + \frac{APR}{n} \right)^n\]

เมื่อ $n$ คือจำนวนครั้งที่มีการแบ่งจ่ายต่อปี

สรุปก็คือธนาคารในปัจจุบันนั้นจะสื่อสารกับลูกค้าด้วยค่า APR ซึ่งแต่ละธนาคารอาจมีนโยบายจ่ายด้วยจำนวนรอบที่ไม่เท่ากัน เช่น ปีละครั้งบ้าง ครึ่งปีบ้าง รายไตรมาสบ้าง ซึ่งตรงนี้ลูกค้าที่ซีเรียสเรื่องดังกล่าวก็ต้องเก็บไปคำนวณเอาเองว่ามันเทียบเท่ากับ EPR ที่เท่าไหร่ (พูดอีกอย่างก็คือธนาคารสื่อสารผิด นั่นคือถ้าจะให้ถูกต้องตามหลักคณิตศาสตร์แล้ว หากธนาคารจ่ายดอกเบี้ย 25% ทุกไตรมาส เช่นนั้นแล้วดอกเบี้ยรวมทั้งปีนั้นคือการนำดอกเบี้ยหนึ่งไตรมาสไปยกกำลังสี่ต่างหาก นั่นก็คือธนาคารจะจ่ายดอกเบี้ยจริงๆ 144.14% ต่อปี ไม่ใช่ว่าจับเอาดอกเบี้ยมาคูณสี่ให้กลายเป็น 25%x4 = 100%)

แต่เอาจริงๆ ในฝั่งลูกค้าก็ไม่จำเป็นต้องไปเครียดกับความไม่ลงรอยกันของตัวเลขระหว่าง APR กับ EPR มากนักหรอก เพราะในโลกความจริงแล้วดอกเบี้ยที่ได้มักมีตัวเลขที่ต่ำมากๆ เช่น APR 1% ซึ่งต่อให้เราซอยย่อยการแบ่งจ่าย-ทบยอดเป็นรายวินาที ผลลัพธ์ก็ยังเป็น EPR 1.005% ที่แทบไม่ต่างจากเดิมเลย (จะเห็นผลต่างก็ต่อเมื่อฝากเงินหลายสิบล้าน ซึ่งจะได้ดอกเบี้ยส่วนต่างระหว่าง APR กับ EPR แค่หลักพันเท่านั้น ทั้งที่ดอกเบี้ยส่วนใหญ่ที่เป็นใจความสำคัญนั้นคือหลักแสน)

แล้วเราควรสนใจความแตกต่างนี้เมื่อไหร่ดี? ก่อนอื่น ถ้าเราลองแทนตัวเลขจำนวนครั้งการแบ่งจ่ายเล่นๆ จะพบว่ามันลู่เข้าค่อนข้างเร็วพอควร เช่น แบ่งจ่ายเป็นรายเดือนกับแบ่งจ่ายรายวันก็แทบไม่ต่างกันแล้ว ดังนั้นเราอาจเปลี่ยนไปสนใจค่าสูงสุดที่เป็นไปได้ของดอกเบี้ยที่จะได้รับ เมื่อเราแบ่งจ่ายเป็นจำนวนครั้งมากๆ (มากจนเข้าใกล้อนันต์ครั้ง) ซึ่งก็คือเราจะสนใจสมการนี้แทน

\[1 - EPR = \lim_{n\to\infty} \left( 1 + \frac{APR}{n} \right)^n\]

จากความรู้เก่าในสมการอันสุดสวยของเรา

\[e = \lim_{n\to\infty} \left( 1 + \frac1{n} \right)^n\]

ทำให้เราจัดรูปฝั่งขวาของสมการได้เป็น

\[\lim_{n\to\infty} \left( 1 + \frac{r}{n} \right)^n = \lim_{n\to\infty} \left( 1 + \frac1{n/r} \right)^n = \left( \lim_{n/r\to\infty} \left( 1 + \frac1{n/r} \right)^{n/r} \right)^r = e^r\]

หรือก็คือสรุปได้ว่า

\[EPR = 1 - e^{APR}\]

ซึ่งถ้าเราทดลองแทนค่า APR ต่างๆ เข้าไปดู จะเห็นว่าแถวๆ ที่ APR = 15% จะได้ EPR = 16% หรือก็คือส่วนต่างของความไม่ลงรอยกันนั้นเริ่มมีค่าเป็น 10% แล้ว ก็น่าจะต้องเริ่มจับตามองจากตรงนี้แหละ(มั้ง?)