อย่ากังวลให้มากไป กับสแตกในฟังก์ชันเวียนเกิด
หนึ่งในไม่กี่เหตุผลที่โปรแกรมเมอร์หลายคนหลบเลี่ยงการเขียนฟังก์ชันเวียนเกิด (recursive function) คงหนีไม่พ้นความกังวลว่าจะไปทำให้สแตกล้น (stack overflow) เพราะโปรแกรมเรียกใช้งานฟังก์ชันซ้อนกันเป็นจำนวนมากเสียเกินกว่าที่สแตกการเรียกฟังก์ชัน (call stack) จะรับไหว จนได้ผลลัพธ์อันน่ารำคาญใจออกมาเป็น Segmentation Fault ในที่สุด
แต่ความกังวลดังกล่าวก็ดูจะทุเลาลงไป เมื่อตัวแปลภาษา (compiler) ฉลาดขึ้นและสามารถรีดประสิทธิภาพของการเรียกฟังก์ชันสุดท้าย (tail call optimization, TCO) ให้กับฟังก์ชันเวียนเกิดที่เขียนมาอย่างเหมาะสม ซึ่งก็คือ ฟังก์ชันที่คืนค่าเป็นการเรียกฟังก์ชันซ้ำไปเรื่อยๆ โดยไม่มีการคำนวณอื่นใดมารบกวน นี่ทำให้ตัวแปลภาษาไม่จำเป็นต้องจองสแตกเพิ่มแต่อย่างใด หน้าที่ของโปรแกรมเมอร์ก็เหลือเพียงแค่การปรับปรุงโค้ดให้รองรับความสามารถดังกล่าวเท่านั้น
ตัวอย่างเช่นโค้ดต่อไปนี้ ที่จะคำนวณ
const f = (n, a=0) => n==0 ? a : f(n-1, a+n)
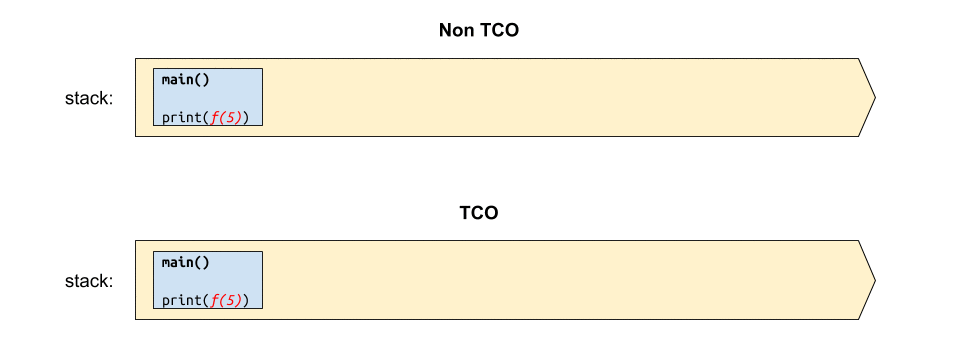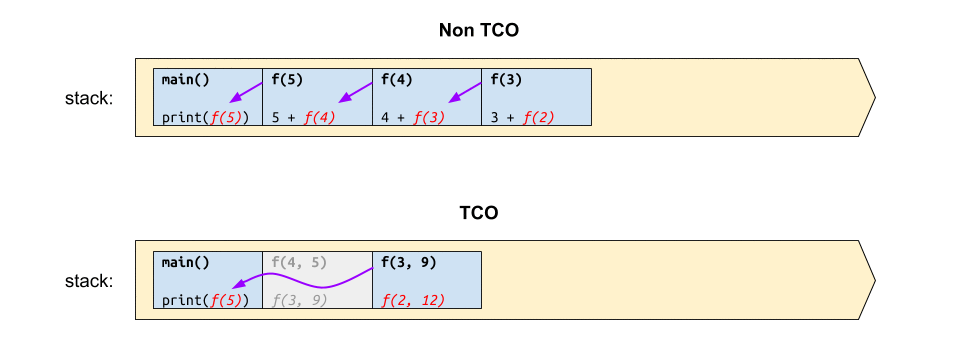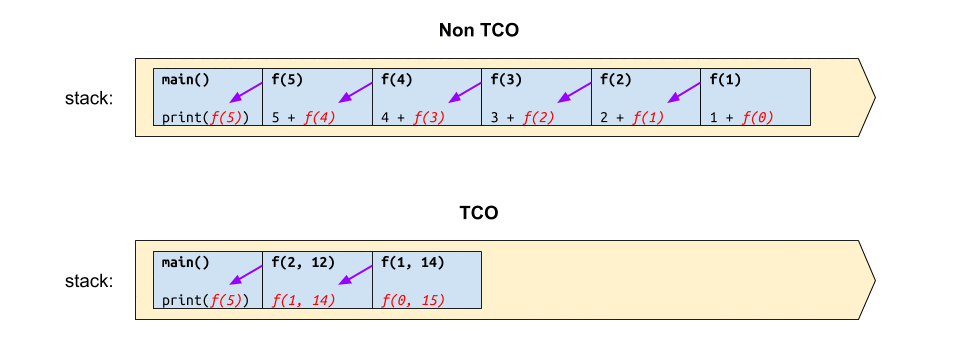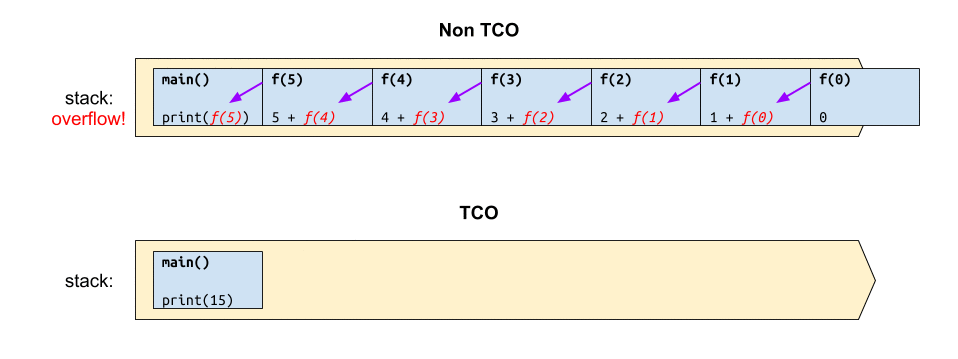
หากวาดภาพการทำงานของฟังก์ชันดังกล่าว เปรียบเทียบกันระหว่างก่อนและหลังทำ TCO ก็คงได้แผนภาพผลลัพธ์ประมาณนี้
จะเห็นว่า ก่อนการทำ TCO นั้น ฟังก์ชันดังกล่าวจะใช้สแตกขนาด
ข้อจำกัดสำคัญของเทคนิค TCO คือ ฟังก์ชันเวียนเกิดจะสามารถเรียกตัวเองได้เพียงครั้งเดียวตอนคืนค่าเท่านั้น แต่อัลกอริทึมในโลกจริงอาจถูกเขียนด้วยฟังก์ชันเวียนเกิดที่เรียกตัวเองซ้ำมากกว่าหนึ่งรอบ เช่น อัลกอริทึมการเรียงแบบเร็ว (quicksort) ที่มีหน้าตาเช่นนี้
const qs = (xs) => {
if (xs.length == 0)
return []
const [p, ...ps] = xs,
ys = ps.filter((x) => x<p),
zs = ps.filter((x) => x>=p)
return [...qs(ys), p, ...qs(zs)] }
นั่นหมายความว่าเราไม่สามารถทำ TCO กับฟังก์ชันเหล่านี้ได้ …
…
ซะที่ไหนกันหละ! เพราะเราสามารถออกแบบฟังก์ชันเวียนเกิดใดๆ ให้คืนค่าเป็นการเรียกตัวเองซ้ำได้เสมอ โดยฟังก์ชันที่เป็นเป้าหมายของเรานี้ จะรับตัวแปรแรกเป็นข้อมูลเพียงครึ่งเดียวของสิ่งที่ต้องทำ พร้อมห่อหุ้ม (closure) ข้อมูลครึ่งหลังไว้เป็นตัวแปรที่สอง ซึ่งถูกส่งต่อให้ตัวเองในอนาคตหยิบมาทำเมื่อพร้อมนั่นเอง
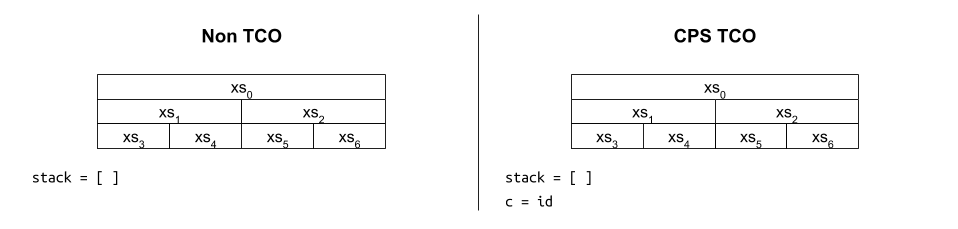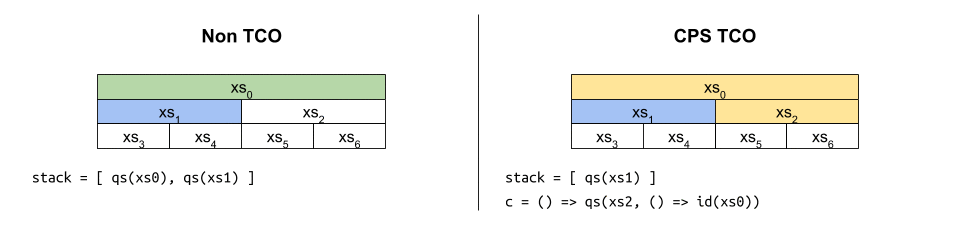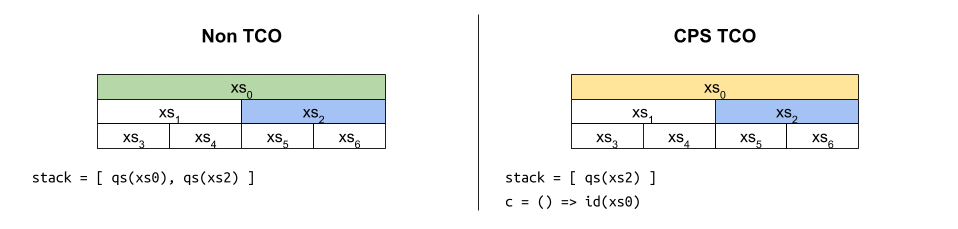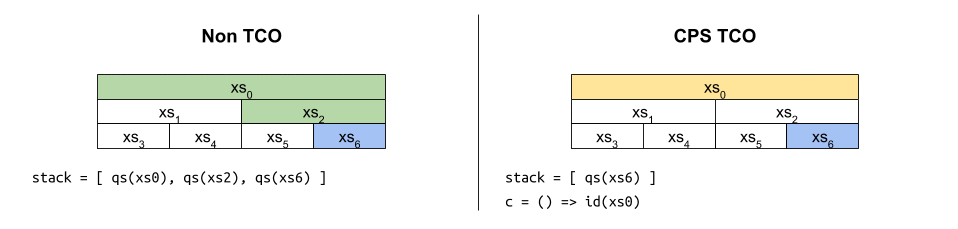
เทคนิคดังกล่าวเรียกว่า การส่งผ่านอย่างต่อเนื่อง (continuation-passing style, CPS) ซึ่งเราสามารถนำมาใช้ปรับโค้ด quicksort ให้อยู่ในรูปแบบดังกล่าวได้ดังนี้
const id = (t) => t
const qs_cps = (xs, c=id) => {
if (xs.length == 0)
return c([])
const [p, ...ps] = xs,
ys = ps.filter((x) => x<p),
zs = ps.filter((x) => x>=p)
return qs_cps(ys, (ls) => qs_cps(zs, (rs) => c([...ls, p, ...rs]))) }
เมื่อไล่การทำงานของมันก็จะได้ภาพประมาณ
แม้ฟังก์ชันดังกล่าวจะเป็น CPS และได้รับประโยชน์จาก TCO ที่คอยควบคุมขนาดของสแตกให้เป็น c ให้ดี จะพบว่ามันถูกห่อหุ้มซ้อนกันมากขึ้นเรื่อยๆ เหมือนงานที่ดองไว้ จนมีขนาดโตเป็น
พูดง่ายๆ ก็คือ เราย้ายสแตกการเรียก (ที่ถูกซ่อนด้วยตัวภาษา) ออกมาให้เห็นกันชัดๆ ในระดับตัวแปรนั่นเอง!
ดังนั้น แม้ว่าเราจะสามารถทำ TCO บนฟังก์ชันเวียนเกิดใดๆ ก็ได้โดยไม่มีใครห้าม แต่ไม่ใช่ทุกการทำ TCO นั้นจะเป็นประโยชน์ แม้เราจะสามารถทำ TCO บนฟังก์ชันเวียนเกิดใดๆ ก็ได้โดยไม่มีใครห้าม แต่ไม่ใช่ทุกการทำ TCO นั้นจะช่วยให้ประหยัดสแตกมากขึ้น อย่าให้ฟังก์ชันใดเห็นแก่พื้นที่สแตกส่วนตัว แต่จงเห็นแก่พื้นที่ RAM ทั้งหมด
เช่นนี้แล้ว ในสายตาของโปรแกรมเมอร์จำนวนหนึ่ง ฟังก์ชันเวียนเกิดคงไม่มีวันเซ็กซี่ เพราะยังไงมันก็สู้การวน while ลูปแบบเดิมๆ ไม่ได้อยู่ดีใช่หรือเปล่า?
… ก็ไม่แน่ ลองย้อนกลับไปเขียน quicksort แบบไม่ง้อการเวียนเกิดดู
const qs_loop = (xs) => {
xs = [...xs]
const stack = [[0, xs.length]]
while (stack.length > 0) {
const [lo, hi] = stack.pop(),
[p, ...ps] = xs.slice(lo, hi),
ys = ps.filter((x) => x<p),
zs = ps.filter((x) => x>=p)
if (ps.length == 0)
continue
xs.splice(lo, ps.length+1, ...ys, p, ...zs)
stack.push([lo, lo+ys.length])
stack.push([hi-zs.length, hi]) }
return xs }
ไม่ว่าอย่างไร เราก็ต้องใช้สแตกเพื่อเก็บสถานะของฟังก์ชันอยู่ดี (แค่เปลี่ยนจากสแตกการเรียกเป็นสแตกตัวแปร) ซึ่งก็กินพื้นที่เป็น
ความน่ากลัวของฟังก์ชันเวียนเกิดจึงไม่ได้อยู่ที่สแตก แต่เป็นการวิเคราะห์และออกแบบอัลกอริทึมให้ใช้พื้นที่อย่างมีประสิทธิภาพมากกว่า เพราะท้ายที่สุดแล้ว ถ้าอัลกอริทึมที่เขียนด้วยฟังก์ชันเวียนเกิดอย่างดีที่สุดยังใช้สแตกจนล้น การเปลี่ยนไปเขียนอัลกอริทึมดังกล่าวด้วยลูปก็ไม่ได้รักษาปัญหานี้ให้หายขาดแต่อย่างใด
-
คิดจากความซับซ้อนเฉลี่ยของ quicksort ที่ต้องเวียนเกิดลงไปลึก
Originally published on: TechJam's Medium