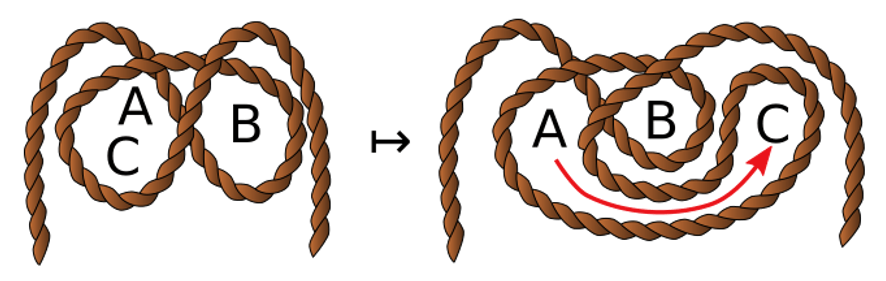TechJam 2018 รอบชิงชนะเลิศ
ถอดใจไปตั้งแต่รอบชิงภาคกลางเพราะเจอแต่เหล่าเด็กเทพมาร่วมงานกันเต็มไปหมด แต่จู่ๆ ก็ได้รับอีเมลบอกว่าผ่านเข้ารอบชิงชนะเลิศระดับประเทศซะงั้น! เลยกลับมาเตรียมตัวกับ @ipats เพื่อรับศึกหนักต่อไป (จะได้ไม่ปล่อยไก่ให้คะแนนเป็นศูนย์อยู่ท้ายตาราง)
ซึ่งทาง TechJam ก็ได้มอบหมายการบ้านให้มาทำ คือเขียนบล๊อกต่อยอดความรู้ความเข้าใจด้านเทคโนโลยี ผมกับ @ipats ในนามทีม monte-carlo เลยส่งบทความสองตอนนี้เข้าร่วมประกวด
ก็บังเอิญอีกว่าได้รับคัดเลือกให้เป็นบทความที่ชนะใจกรรมการ (พร้อมกับน้อง @AquaBlitz11 อีกทีม) ทั้งที่มองซ้ายมองขวาดูแล้วบล็อกของทีมอื่นๆ ก็มีที่เจ๋งๆ อีกเยอะเลย (อ่านบทความทั้งหมดของทีมที่ส่งประกวดได้ที่ @TechJamThailand) ก็เลยได้สิทธิพิเศษในการแข่งบางอย่าง ที่จะไปเฉลยว่าคืออะไรในวันจริง …
เนื่องจากว่าวันนั้นเบลอๆ เพราะนอนน้อย เลยจำโจทย์ได้ไม่หมด (จนไม่แน่ใจว่าที่จดๆ ไว้นี่คือจำโจทย์ถูกหรือเปล่า 555) ก็เอาเท่าที่ได้ละกันนะ
ข้อเล็กๆ ถามสั้นตอบไว
ไม่แน่ใจว่าคำถามแบบสัญชาติญาณที่ให้เขียนคำตอบลงไวท์บอร์ดในเวลาไม่ถึงนาที มันบีบคั้นหัวใจเกินไปหรืออย่างไร เพราะในรอบชิงชนะเลิศนี้กรรมการได้ตัดการแข่งขันดังกล่าวทิ้งไปเลย คงเหลือไว้แต่ข้อที่ต้องเขียนโปรแกรมแก้ปัญหาให้ทันภายใน 5 นาทีเท่านั้น
เนื่องจากมีทีมเข้าร่วมแข่งขัน 20 ทีม แต่มีโพเดียมแค่ 10 ตัวเท่าเดิม ก็เลยต้องมาสุ่มกันว่าจะเจอคู่แข่งเป็นทีมใดบ้าง และเนื่องจากกรรมการไม่ต้องการแยกห้องทีมที่กำลังแข่งกับทีมที่นั่งรอแล้ว แต่อยากให้ทีมที่เหลือนั่งเชียร์ (และสนุกกับคำถามของ) ทีมที่กำลังแข่งไปพร้อมกันเลย จึงมีโจทย์ทั้งหมด 12 ข้อ แบ่งเป็น 4 ชุด ให้แต่ละทีมลุ้นกันว่าจะได้เจอกับคำถามอันสุดโหดหิน 2 ชุดไหน
และนี่คือสิทธิพิเศษจากการทำการบ้านเขียนบล็อก ซึ่งก็คือทีมเราจะสามารถเลือกสลับชุดคำถามกับทีมไหนก็ได้! (แต่ไม่เห็นคำถามล่วงหน้านะ)
ด้วยความที่คิดไม่ออกว่าจะสลับที่กับทีมไหนดี (@AquaBlitz11 เลือกสลับที่ไปก่อนแล้วในคำถามชุดแรก) เมื่อถึงช่วงก่อนเริ่มคำถามชุดที่สอง กรรมการก็เปิดให้ใช้สิทธิ์สลับที่อีกครั้ง ตอนนั้นนึกออกเลาๆ ว่าจากที่อ่านมาในบล็อกบันทึกการแข่งของ @AquaBlitz11 ดูน้องเค้าค่อนข้างกลัว “Team ↓↓↓ Second Place ↓↓↓” (ชื่อทีมหรือนั่น?) ที่เป็นแชมป์ภาคเหนือพอสมควร แถมพอสลับที่ไปแล้วจะได้อยู่ติดกับทีม “Meow Meow :3” ที่ยืนโพเดียมข้างๆ กันมาตั้งแต่รอบชิงภาคกลางอีกด้วย (และจะได้นั่งพักดูทีมอื่นเล่นก่อน ลดความตื่นเต้นไปด้วยในตัว) ก็เลยเลือกสลับที่ไปเช่นนั้น …
ไม่รู้ว่าสลับที่ไปแบบนี้คือช่วยหรือเตะตัดขา @AquaBlitz11 กันแน่ ซึ่งถ้าเป็นอย่างหลังก็ขออภัยด้วยนะ 🙏
มาดูโจทย์กันเลยดีกว่า!
แขวนภาพไม่ระวัง
เกริ่นก่อนว่าเวลาเราแขวนภาพเนี่ย เราก็อยากจะแขวนมันดีๆ ไม่ให้ร่วงจากผนังง่ายๆ ซึ่งก็อาจทำได้ด้วยการแขวนภาพด้วยเชือกที่พาดผ่านตะปูหลายๆ ตัวหน่อย
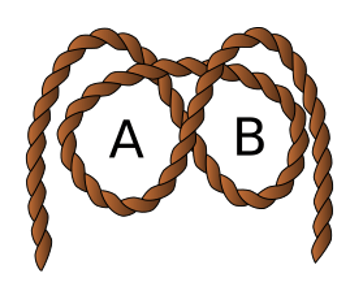
แต่นักคณิตศาสตร์ในสายทฤษฎีปมเงื่อน (knot theory) คงไม่คิดเช่นนั้น เพราะพวกเขาถามในสิ่งที่ขัดกับสามัญสำนึกของคนส่วนใหญ่ โดยถามว่าจะแขวนรูปภาพบนตะปูสองตัวยังไง ทีเมื่อตะปูตัวหนึ่งหลุดออกมาแล้ว ภาพที่แขวนไว้ก็จะหล่นลงมาทันทีโดยไม่ต้องไปยุ่งกับตะปูตัวที่สอง1
ตัวอย่างการแขวนรูปบนตะปูสองตัว (A, B) โดยไม่ว่าจะดึงตะปูตัวไหนออก ภาพก็จะหล่นลงมาจากผนัง
ส่วนคำถามสำหรับการแข่งขันครั้งนี้ คือ ให้หารูปแบบของเชือกที่พาดผ่านตะปูสามตัว (เรียงลำดับว่า A, B, C) ที่ตรงตามเงื่อนไขต่อไปนี้
- ดึงตะปู A หรือ C ออกแค่ตัวเดียวแล้วภาพยังแขวนอยู่
- ดึงตะปู A และ C ออกทั้งสองตัวแล้วภาพหล่นลงมา
- ดึงตะปู B ออกแค่ตัวเดียวแล้วภาพหล่นลงมา
ข้อนี้เกือบจะทำได้แล้วโดยการเอาภาพตัวอย่างที่กรรมการให้ (ตะปู 2 ตัว) มาดัดแปลงแล้วตอบอย่างรวดเร็ว แต่ด้วยความรีบลนก็ดันผลิตบั๊กในตอนจบซะได้ … ซึ่งอันที่ถูกต้องควรจะทำแค่นี้
คำตอบของการแขวนรูปข้างต้น หรือเขียนแทนด้วยสัญลักษณ์พาดเชือกทวน/ตามเข็มว่า
อาเรย์จุดตรึง
โจทย์ถามว่า มีอาเรย์ความยาว 20 ตัวอยู่กี่อาเรย์ ที่จะผ่านการตรวจสอบของฟังก์ชันนี้?
function validate(ls) {
all(1 <= ls & ls <= length(ls) & diff(ls) >= 0 & ls == ls[ls])
}
โอเค ก่อนอื่นมาทำความเข้าใจฟังก์ชันตรวจสอบนี้กันก่อน (การแข่งจริงให้โค้ดเทียมมา ไม่ใช่ภาษา R เช่นนี้) สองเงื่อนไขแรกบอกว่าอาเรย์สามารถเก็บค่าของตำแหน่ง (index) ที่เป็นไปได้ในอาเรย์ดังกล่าวเท่านั้น (เริ่มนับตำแหน่งที่ 1) และเงื่อนไขต่อมาบอกว่าอาเรย์ต้องเป็นแบบที่มีค่าไม่ลด (non-decreasing)
เงื่อนไขที่น่าสนใจที่สุดก็คือข้อสุดท้าย ที่บอกว่าสมาชิกตัวใดๆ ในอาเรย์ (สมมติว่าตอนนี้กำลังสนใจตำแหน่งที่ i ซึ่งมีค่าเป็น ls[i]) เมื่อเอาไปหาอาเรย์ที่ตำแหน่งของค่าสมาชิกตัวนั้น (ls[ls[i]]) ค่าทั้งสองจะต้องมีเท่ากันด้วย (ls[i] == ls[ls[i]])
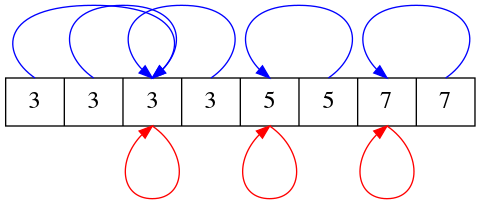
เช่น ถ้าสมาชิกตัวที่เราสนใจมีค่าเป็น 3 แปลว่าอาเรย์ช่องที่ 3 ต้องมีค่าเป็น 3 ด้วย
หนึ่งในตัวอย่างอาเรย์ที่ตรงตามเงื่อนไขข้างต้น
นี่ทำให้เราเห็นได้ทันทีว่า อาเรย์จะต้องมีจุดตรึง (fixed point) อย่างน้อยหนึ่งจุด ซึ่งก็คือจุดที่สมาชิกในตำแหน่งนั้นมีค่าเท่ากับตำแหน่งที่มันอยู่ด้วยนั่นเอง
ดังนั้น ทางเลือกของสมาชิกแต่ละตัวในอาเรย์คือ
- สมาชิกตัวนั้นมีค่าเท่ากับตำแหน่งที่มันอยู่พอดี
- สมาชิกตัวนั้นมีค่าเท่ากับสมาชิกในตำแหน่งก่อนหน้า
- สมาชิกตัวนั้นมีค่าเท่ากับสมาชิกในตำแหน่งถัดไป
เมื่อนำข้อสังเกตดังกล่าวมาสร้างตารางแจกแจงอาเรย์ทั้งหมดที่เป็นไปได้ โดยเปรียบเทียบความยาวอาเรย์กับสมาชิกตัวสุดท้าย ก็จะได้ดังนี้
หรือเขียนเป็นความสัมพันธ์เวียนเกิดได้ว่า
เมื่อ
ถึงตอนนี้ถ้ายังมีแรงไล่ต่อไปอีก อาจจะพบว่า
โอโหหห ข้อนี้ยากมากกกกกก ไม่มีทีมไหนตอบได้เลย ให้ลงไปแข่งด้วยก็มองไม่ออก กลับมานั่งโซ้วกว่าจะได้คำตอบก็อีกหลายวันให้หลัง ถถถ
ตารางมหัศจรรย์
ข้อนี้โจทย์สั้นๆ คือขอให้เติมตารางขนาด
นี่คือโจทย์เก่าแก่นามว่าจัตุรัสกล (magic square) ที่ย้อนรอยกลับไปได้ไกลถึงสองพันปีที่ประเทศจีน!! ซึ่งไอ้การรู้ชื่อรู้โจทย์รู้ประวัตินั้นไม่ได้เป็นเรื่องสลักสำคัญอะไรเลยเมื่อจำวิธีแก้มันไม่ได้ 😂
(ถ้าจำไม่ผิด โจทย์ในการแข่งก็ไม่ได้ถามหาจัตุรัสกลซะทีเดียว เพราะขาดเงื่อนไขผลรวมแนวทะแยง)
ด้วยความเบลอและคิดว่าโค้ดไม่ทันแน่ๆ (ถึงแม้จะโค้ดทันก็คงรัน
แต่ทีม Meow Meow :3 ที่ยืนข้างกันดันตอบได้! พอถามดูแล้วพบว่าใช้ภาษา Zinc (ไม่แน่ใจว่า dialect ไหน) ซึ่งเป็นภาษาเชิงเงื่อนไข (ญาติกับภาษาเชิงตรรกะอย่าง Prolog) ในการแก้โจทย์ข้อนี้ หลังการแข่งขันเสร็จก็คันไม้คันมือ เลยไปหา MiniZinc มาศึกษาดูบ้าง ซึ่งจะเขียนเฉลยจัตุรัสกลได้ประมาณนี้
int: n = 4;
set of int: idxs = 0..n-1;
var int: x;
array[idxs,idxs] of var 1..pow(n,2): t;
constraint forall(r1,r2 in idxs, c1,c2 in idxs) (
r1 == r2 /\ c1 == c2 <-> t[r1,c1] == t[r2,c2]
);
constraint forall(r in idxs) (
x == sum(c in idxs)(t[r,c])
);
constraint forall(c in idxs) (
x == sum(r in idxs)(t[r,c])
);
constraint forall(i in idxs) (
x == sum(j in idxs)(t[j,(n+i+j) mod n])
);
constraint forall(i in idxs) (
x == sum(j in idxs)(t[j,(n+i-j) mod n])
);
solve satisfy;
output [
show_int(2, t[r,c]) ++ (if c == n-1 then "\n" else " " endif)
| r in idxs, c in idxs
];
รันเร็วมาก! ไม่รู้ว่ามันลดทอนขอบเขตของการค้นหาคำตอบยังไง เพราะแค่สั่งทำงานไปได้ไม่ถึงครึ่งวินาทีก็ได้รับคำตอบนี้กลับมา
การสัมผัสกันของ Tetromino
Tetromino คือตัวต่อในเกม Tetris ที่มีอยู่ทั้งหมด 7 แบบ (มีชื่อเรียกตามรูปร่างด้วยนะ คือ I, O, T, S, Z, J, L … โดยเจ้าตัวสุดท้ายเคยชนะโหวตตัวละครยอดเยี่ยมปี 2007 บน GameFAQs เลยทีเดียว!) ถ้าเราจับเหล่า tetromino มาบรรจุลงกล่อง นี่อาจเป็นหนึ่งในคำตอบที่เป็นไปได้
ตัวอย่างการสัมผัสกันของ tetromino (ไม่นับรวมขอบนอกสุด) ที่มีความยาวรวมเท่ากับ 35 หน่วย
ถามว่า ให้กล่องขนาด
ข้อนี้ @ipats คิดออกอย่างรวดเร็ว … เสียดายว่าไม่ได้อยู่ในรอบที่ตัวเองแข่งเลยอดได้คะแนนฟรี ซึ่งคำตอบของกรณีน้อยที่สุดก็คือพยายามใส่ตัว O ลงไปจนใส่ไม่ได้ (เพราะเส้นรอบรูปยาวน้อยสุด) แล้วค่อยถมด้วยตัว I ส่วนคำตอบของกรณีมากสุดคือถมด้วยตัวอะไรก็ได้ที่ไม่ใช่ตัว O (เพราะเส้นรอบรูปตัวที่เหลือยาวเท่ากัน) ซึ่งเอาง่ายๆ ก็คือถมด้วยตัว I อย่างเดียวไปเลย
ดังนั้นตอบว่าสัมผัสกันน้อยสุด 90 หน่วย และสัมผัสกันมากสุด 114 หน่วย
พ่อค้าเร่ผู้โชคร้าย
เชื่อว่าผู้ชื่นชอบการแก้ปริศนาและนักศึกษาสายคณิตศาสตร์/คอมพิวเตอร์ คงไม่มีใครไม่รู้จักกับปัญหาพ่อค้านักเดินทาง (travelling salesman problem, TSP) ที่ถามว่า ให้เมืองมาจำนวนหนึ่งบนแผนที่ จงหาเส้นทางที่สั้นที่สุดที่จะเดินทางไปค้าขายจนครบทุกเมืองพร้อมวกกลับมายังเมืองบ้านเกิด
ถึงปัญหาจะเป็น NP-hard และการหาคำตอบที่ดีที่สุดนั้นกินเวลาเกินกว่าที่จะรับได้ แต่เราก็มีอัลกอริทึมสำหรับประมาณที่ทำงานได้เร็วกว่าเพียงแค่แลกมาด้วยความใกล้เคียงของคำตอบที่ดีที่สุด หนึ่งในอัลกอริทึมนั้นเป็นแบบละโมบซึ่งมีขั้นตอนวิธีดังนี้
- เดินทางไปยังเมืองที่ใกล้ที่สุดที่ยังไม่เคยไป (ไปเมืองใดก็ได้หากมีเมืองที่ห่างเท่ากันหลายเมือง)
- ทำซ้ำข้อ 1. ไปเรื่อยๆ จนกว่าจะเดินทางไปครบทุกเมือง
- เดินทางเป็นเส้นตรงจากเมืองสุดท้ายกลับมายังเมืองบ้านเกิด
จะเห็นว่าจุดอ่อนที่สุดของอัลกอริทึมนี้อยู่ในขั้นตอนที่ 3 ที่เดินทางกลับตรงๆ โดยไม่ใจว่าเคยเดินทางผ่านเมืองใดมาแล้วบ้าง ซึ่งมันจะให้ผลลัพธ์ที่แย่ที่สุดแย่เป็น
คำถามคือ เมื่อให้เมืองที่อยู่บนกริดขนาด
เหมือนว่ากรรมการจะมองออกว่าการให้วาดคำตอบบนไวท์บอร์ดนั้นมีความยุ่งเหยิงสูงและตรวจยาก เลยแจกกระดาษคำถามหนึ่งแผ่นที่จุดเมืองต่างๆ เตรียมไว้แล้วพร้อมปากกามาให้ลากคำตอบแทน (แต่ก็ไม่ได้แจกเป็นดินสอ-ยางลบเพราะคงไม่อยากให้ทดในนี้หละมั้ง?) … ก็น่าเสียดายว่าลากคำตอบที่คิดแว๊บแรกว่าถูกไปเรียบร้อยแล้ว แต่พอยืนคิดทบทวนอีกรอบมันดันไม่ถูกซะหนิ ส่วนคำตอบที่ถูกต้องคือ
เส้นทางนี้ยาว
หน่วย
หารหัสตู้เซฟ
ให้ตู้เซฟ (ที่ไม่ค่อยจะเซฟซักเท่าไหร่) มาตู้หนึ่ง โดยเมื่อเรากดรหัส 6 ตัวเสร็จ ตู้เซฟจะตอบกลับมาว่าเรากดรหัสเรียงกันถูกต้องมากที่สุดทั้งหมดกี่ตัว ให้หารหัสที่เปิดตู้เซฟได้จากข้อมูลต่อไปนี้
เหมือนจะยากจนไม่น่าเขียนโปรแกรมทันในห้านาที แต่จริงๆ แล้วเกมนี้คล้ายกับ Mastermind และด้วยข้อมูลตามข้างต้นก็สามารถคิดในใจได้เลย … เสียดายว่าไม่ได้อยู่ในรอบตัวเองอีกแล้วเพราะ @ipats คิดออก
โดยวิธีคิดสำหรับข้อนี้ คือ
- พิจารณาข้อมูลที่บอกว่ารหัสที่ใส่ไม่มีตัวใดถูกเลย จะได้ว่า
- ดูตัวที่ถูกต้องติดกันยาวที่สุด (ยาว 3) แล้วตัดเลขที่เป็นไปไม่ได้แน่ๆ ออกไป จะได้ว่า
- จาก
- จาก
- จาก
- ไล่ดูต่อจะพบว่า
- สังเกตว่า
- แต่จากข้อมูลของรหัสที่ถูกยาว 1 ตัว เมื่อดูแล้วจะพบว่ารหัสที่เขียนในรูป
- แต่จากข้อมูลของรหัสที่ถูกยาว 1 ตัว เมื่อดูแล้วจะพบว่ารหัสที่เขียนในรูป
- ดังนั้นจะเหลือเพียง 2 ตัวเลือก คือ
- แต่จากข้อมูลของรหัสที่ถูกยาว 1 ตัว จะทำให้
- แต่จากข้อมูลของรหัสที่ถูกยาว 1 ตัว จะทำให้
ดังนั้นข้อนี้ตอบ
ผลรวมจำนวนเฉพาะ
น่าจะเป็นโจทย์ที่ง่ายที่สุดในการแข่งขันนี้แล้ว เพราะโจทย์ต้องการให้หาจำนวนเฉพาะที่อยู่ติดกันที่มีผลรวมเท่ากับหนึ่งล้านพอดี โดยให้ตอบคำถามดังกล่าว 3 อย่าง คือ จำนวนเฉพาะตัวแรก จำนวนเฉพาะตัวสุดท้าย และขนาดของจำนวนเฉพาะว่ามีกี่ตัว?
from itertools import count
from extmath import primes # pip install extmath
for i in count():
acc = 0
j = i
while acc < 10**6:
acc += primes[j]
j += 1
if acc == 10**6:
print(primes[i], primes[j-1], len(primes[i:j]))
break
ควรจะได้คะแนนฟรี! แต่ตอนแข่งดันคุมความตื่นเต้นไม่อยู่ ไปพิมพ์เครื่องหมาย <= แทนที่จะพิมพ์แค่ < ตามโค้ดข้างต้นซะได้ … แต่ถึงจะแก้บั๊กตรงนั้นทัน ก็คิดว่ายังไงคงไม่ได้คะแนนข้อนี้จริงๆ แหละมั้ง เพราะทีมอื่นก็ตอบจำนวนเฉพาะตัวสุดท้ายผิดบ้าง นับความยาวผิดบ้าง (ความผิดในกลุ่ม off-by-one error ทั้งนั้น ไม่ได้เกี่ยวกับตัวอัลกอริทึมเลย …) แล้วมีหรือที่เราในสถานการณ์นั้นจะไม่ตกหลุมพรางเหล่านี้ต่อ 😅
หาเพื่อนร่วมห้อง
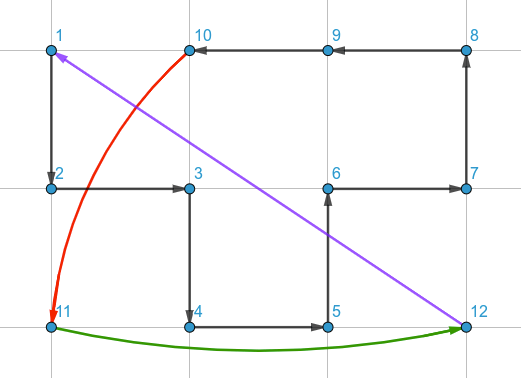
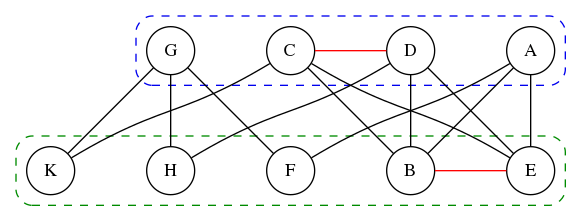
โจทย์สนใจโรงเรียนแห่งหนึ่งที่มีนักเรียน 9 คน แบ่งเป็น 2 ห้อง และมีความสัมพันธ์การอยู่ร่วมห้องกันดังนี้
ในความสัมพันธ์นี้มี 2 ข้อที่ผิด ถามว่าคือข้อไหนบ้าง และเมื่อแก้ไขแล้ว
… ด้วยความตื่นเต้นกดดัน ก็มัวแต่นั่งไล่ความสัมพันธ์ผ่านคีย์บอร์ดคอมพิวเตอร์ (เพราะ @ipats ใช้ไวท์บอร์ดคิดไปพร้อมๆ กันอยู่) ทั้งที่คำถามแนวนี้มันควรจะต้องเปิดโปรแกรมวาดรูปขึ้นมาลากเส้นดูด้วยซ้ำ (แต่ให้วาดรูปผ่านทัชแพดก็น่าจะไม่รอดอยู่ดี) เลยพลาดที่จะเห็นความสัมพันธ์อันเรียบง่ายชัดเจนของกราฟสองส่วน อดได้คะแนนฟรีๆ ไปอีกหนึ่งข้อ …
กราฟสองส่วนที่แสดงให้เห็นว่าใครอยู่ห้องไหน โดยมีเส้นสีแดงแทนความสัมพันธ์ที่ผิด
กรรมการไม่ได้บอกว่าให้เอากระดาษปากกาเข้ามาแข่งได้ ก็สงสัยว่าโน๊ตบุ๊คเครื่องหน้าต้องซื้อแบบมีปากกาสไตลัสแล้วหละสิ 🤔
ข้อใหญ่ๆ แก้โจทย์สนใจ Big-O
การแก้ปัญหาแบบเน้นอัลกอริทึมในรอบนี้มีด้วยกันถึง 4 ข้อ โดย 3 ข้อแรกเป็นโจทย์แนวเดิม คือ โจทย์วัดความสามารถในการเลือกใช้อัลกอริทึมที่เหมาะสมและหาคำตอบที่ถูกต้องได้ทันท่วงที (มีข้อมูลนำเข้าชุดเล็ก/ใหญ่แบบเดียวกับ Google Code Jam)
ส่วนโจทย์อีกข้อเป็นของใหม่ ซึ่งมีลักษณะเป็นคำถามปลายเปิดที่วิธีหาคำตอบอาจจะไม่ยากมาก แต่เราต้องพยายามลดขั้นตอนระหว่างทางเพื่อไปให้ถึงคำตอบให้เหลือน้อยครั้งที่สุด
น่าเสียดายว่ากรรมการพิมพ์เทสเคสโจทย์ข้อ 2 ผิดไปหนึ่งตัว และก็อาจจะรวมกับเนื้อหาโจทย์ที่ชวนงงด้วย จึงไม่มีใครทำโจทย์ข้อ 2 เลย (อย่างน้อยก็ก่อนที่จะฟรีซตารางคะแนนของผู้เข้าแข่งขันก่อนหมดเวลาแข่งครึ่งชั่วโมง)
ด้วยความติดบั๊กและถอดใจ เลยทำไปได้แค่ 2 ข้อ ซึ่งก็คือข้อแรกและข้อสุดท้ายเท่านั้น
อุกกาบาตถล่มเกาะ
โจทย์ให้เกาะมาหนึ่งเกาะซึ่งมีลักษณะพิเศษ คือ ไม่ว่าจะอยู่ตรงส่วนไหนของเกาะก็จะสามารถมองเป็นเส้นตรงไปยังตำแหน่งอื่นๆ บนเกาะได้เสมอ … อยู่มาวันหนึ่งมีอุกกาบาตจำนวนมากจะพุ่งเข้าชนเกาะ หลังจากทีมนักฟิสิกส์ได้คำนวณตำแหน่งที่คาดว่าจะตกของอุกกาบาตชิ้นต่างๆ เรียบร้อยแล้ว จงตอบว่าอุกกาบาตชิ้นหนึ่งๆ จะตกลงมาบนเกาะพอดีหรือไม่ เพื่อส่งข้อมูลต่อให้ฝ่ายความมั่นคงเลือกยิงขีปนาวุธอย่างประหยัดต่อไป
โจทย์ให้เวลา 1 วินาที (Java เวลาคูณ 2, Python เวลาคูณ 4) พร้อมข้อจำกัดต่างๆ ดังนี้
- เคสง่าย เกาะจะมีมุม
- เคสยาก เกาะจะมีมุม
หลังจาก @ipats อ่านและตีความโจทย์จนเข้าใจ ก็สรุปว่าโจทย์ต้องการทดสอบว่าจุดที่ให้มานั้นอยู่ในโพลิกอนของเกาะหรือเปล่า?
ฟังถึงแค่นี้ก็ไล่ @ipats ให้ไปอ่านโจทย์ข้ออื่นต่อเลย แล้วลงมือโค้ดสิ่งนี้ออกมาอย่างรวดเร็ว …
from collections import namedtuple
Point = namedtuple('Point', 'x y')
Point.from_string = lambda s: Point(*map(int, s.split()))
def ccw(u, v, w):
det = u.x*v.y + v.x*w.y + w.x*u.y - u.y*v.x - v.y*w.x - w.y*u.x
return 1 if det > 0 else -1 if det < 0 else 0
def half_hull(points):
hull = []
for point in points:
while len(hull) >= 2 and ccw(hull[-2], hull[-1], point) > -1:
hull.pop()
hull += [point]
return hull
def convex_hull(hull):
upper_hull = half_hull(hull)
lower_hull = half_hull(reversed(hull))
return upper_hull + lower_hull[1:]
def inner_hull(hull, check):
possible_edge = False
for p, q in zip(hull, hull[1:]):
clock = ccw(p, q, check)
if clock == 0:
possible_edge = True
if clock == 1:
return 'Outside'
return 'Inside' if not possible_edge else 'On the boundary'
def main():
hull = convex_hull(sorted(Point.from_string(input()) for _ in range(int(input()))))
for check in (Point.from_string(input()) for _ in range(int(input()))):
print(inner_hull(hull, check))
if __name__ == '__main__':
main()
แน่นอนว่าโค้ดนี้ส่งผ่านแค่เคสเล็ก แต่ก็ทำให้อุ่นใจขึ้นมามากๆ หลังจากที่ช่วงเช้าไม่ได้เลยซักคะแนน หลังจากนั้นจึงมาดูว่าจะเร่งโค้ดให้เร็วตรงไหนได้บ้าง
เนื่องจากโพลิกอนที่โจทย์ให้มาเป็นโพลิกอนแบบพิเศษที่มีชื่อว่าคอนเวกซ์ฮัลล์ เรามีท่าต่างๆ เพื่อเร่งความเร็วการทดสอบนี้ได้ เช่น มองฮัลล์ดังกล่าวเป็นรูปสี่เหลี่ยมคางหมูแล้วค้นหาแบบทวิภาคว่าจะใช้สี่เหลี่ยมคางหมูชิ้นไหนมาตรวจสอบ
แต่ไม่ว่าจะแก้โค้ดเปลี่ยนอัลกอริทึมเท่าไหร่ก็ส่งคำตอบไม่ผ่านซักที (เพิ่งมาเห็นทีหลังด้วยว่าโจทย์เรียงลำดับจุดในฮัลล์มาให้แต่แรกแล้ว) ไม่รู้ด้วยว่าใช้เวลาดีบั๊กไปนานเท่าไหร่ ส่วนนี่คือโค้ด Python รุ่นสุดท้ายก่อนที่จะถอดใจ (ก็ดูว่ามันรันในเวลา
from collections import namedtuple
Point = namedtuple('Point', 'x y')
Point.from_string = lambda s: Point(*map(int, s.split()))
def ccw(u, v, w):
det = u.x*v.y + v.x*w.y + w.x*u.y - u.y*v.x - v.y*w.x - w.y*u.x
return 1 if det > 0 else -1 if det < 0 else 0
def aux(hull, check, lo, hi):
mid = (lo+hi+1) // 2
if lo+1 == hi:
return hull[lo], hull[hi]
fst, snd = (lo, mid) if check.x <= hull[mid].x else (mid, hi)
return aux(hull, check, fst, snd)
def bisect(hull, check):
lo = 0
hi = len(hull) - 1
if check.x == hull[lo].x:
return hull[lo], hull[lo+1]
if check.x == hull[hi].x:
return hull[hi-1], hull[hi]
return aux(hull, check, lo, hi)
def inner_hull(upper_hull, lower_hull, check):
ui, uj = bisect(upper_hull, check)
li, lj = bisect(lower_hull, check)
for p, q in [(ui, uj), (lj, li)]:
if p.x == q.x:
if p.y <= check.y <= q.y or q.y <= check.y <= p.y:
return 'On the boundary'
else:
return 'Outside'
else:
clock = ccw(p, q, check)
if clock == 0:
return 'On the boundary'
if clock == 1:
return 'Outside'
return 'Inside'
def read_hull():
upper_hull, lower_hull = [], []
go_low = False
for _ in range(int(input())):
point = Point.from_string(input())
if not upper_hull:
upper_hull += [point]
elif go_low:
lower_hull += [point]
elif upper_hull[-1] > point:
if upper_hull[-1].x == point.x:
lower_hull += [upper_hull[-1]]
lower_hull += [point]
go_low = True
else:
upper_hull += [point]
lower_hull += [upper_hull[0]]
return upper_hull, lower_hull[::-1]
def main():
upper_hull, lower_hull = read_hull()
for check in (Point.from_string(input()) for _ in range(int(input()))):
print(inner_hull(upper_hull, lower_hull, check))
if __name__ == '__main__':
main()
ด้วยความเชื่อมั่นว่าอัลกอริทึมถูกแน่นอน เลยเปลี่ยนไปเขียนด้วย C++ ที่เคยถนัด … คราวนี้บั๊กกระจายเลย หัวร้อนยิ่งกว่าเก่าจน @ipats ต้องมาสะกิดให้เปลี่ยนไปทำข้ออื่น 😭
(แข่งเสร็จกลับมาทดลองอัลกอริทึมกับข้อมูลนำเข้าที่สร้างเอง พบว่าอัลกอริทึมใน Python มันก็รันทันในเวลาที่ให้นะ … หรือว่าเครื่องเราแรงกว่าเครื่องเซิร์ฟเวอร์ที่ใช้แข่งเนี่ย??)
ไม่ว่ายังไง … รู้สึกว่าสกิล Python ในการแข่งขันพวกนี้มันมาถึงทางตันซะแล้วสิ ถ้ายังอยากเอาดีด้านนี้ต่อไป คงต้องกลับไปใช้ C++ ให้คล่องจนสามารถโค้ดได้จากไขสันหลังแล้วหละมั้ง 🤩
หมุนแล้วเรียง เรียงแล้วหมุน
ลองจินตนาการถึงโลกที่การสลับที่ของเป็นกลุ่มๆ นั้นรวดเร็วกว่าการสลับของทีละชิ้น กล่าวคือ เรามีฟังก์ชันการหมุนสลับที่ของสิ่งของ
ให้พิมพ์ทุกๆ
ระหว่างที่พยายามรีดความเร็วให้ข้อแรกอยู่ @ipats ก็คิดข้อนี้ออกและแนะนำให้เขียนเอาคะแนนฟรีๆ ไปก่อน โดยแนวคิดหลักๆ จะเหมือนการเรียงลำดับแบบฟอง (bubble sort) คือไล่เอาสมาชิกตัวที่มีค่าต่ำสุดที่ยังไม่ได้เรียงขึ้นมาไว้ข้างหน้าของอาเรย์เรื่อยๆ โดยในแต่ละรอบที่สลับเอาของไปไว้ข้างหน้า จะใช้ฟังก์ชันหมุนสลับที่ที่โจทย์ให้มาอยู่ 2 ครั้ง ตามโค้ดนี้
swap = lambda ls, i, j: ls[j:] + ls[i:j] + ls[:i]
n = int(input())
ls = [int(input()) for _ in range(int(n))]
rs = sorted(ls)
i = 0
answers = []
while i < n:
j = ls.index(rs[i], i)
if i != j:
answers += [(i, j)]
ls = swap(ls, i, j)
answers += [(0, n-i)]
ls = swap(ls, 0, n-i)
i += 1
print(len(answers))
for i, j in answers:
print(i+1, j)
จะเห็นได้ทันทีว่าวิธีนี้ให้คำตอบที่แย่ที่สุดไม่เกิน
สรุป
งานสนุกดีครับ ได้มาดูออฟฟิศสวยๆ ของ KBTG ด้วย (เข้าใจว่าอยากโชว์ของดีของเด็ดในมือเต็มที่ 😉) ได้เปิดโลกรู้จักอัลกอริทึมแปลกๆ ภาษาที่ไม่เคยแม้แต่จะได้ยินชื่อกระบวนทัศน์ ไปจนถึงแขนงวิชาและการวิจัยทางคณิตศาสตร์/คอมพิวเตอร์ที่อยู่สุดขอบความรู้ของมนุษยชาติ
และสิ่งที่สำคัญที่สุด ก็คงหนีไม่พ้นการได้พบปะเพื่อนใหม่ผู้มีฝีมือระดับทะลุชั้นบรรยากาศมากมาย อันได้แก่ (แต่ไม่จำกัดเพียง) @AquaBlitz11 เหรียญทองแดง IOI ปีนี้, Bonmek ผู้ชนะจากภาคใต้ที่ฝีไม้ลายมือไม่ธรรมดา, need-more-papers ทีมซุ่มเงียบที่เพิ่งจะรู้ว่ามาจากม.เกษตรฯ เช่นเดียวกัน, Meow Meow :3 ทีมผู้ชนะ (ที่ก็ดูจะตกใจไม่น้อยเมื่อได้ยินประกาศชื่อตัวเอง) ก็หวังว่าจะได้ยินชื่อพวกนายในฐานะแนวหน้าของวงการอีกบ่อยๆ นะ
ขอบคุณ KBTG อีกครั้งที่จัดงานดีๆ แบบนี้ขึ้นมา หวังว่าจะเป็นแรงกระเพื่อมครั้งใหญ่ที่กระเพื่อมต่อไปอย่างไม่หยุดหย่อน คอยผลักดันวงการเทคโนโลยีของไทยให้ก้าวไกลทัดเทียมระดับโลกครับ
ท้ายที่สุด ขอบคุณ @ipats อีกครั้งที่สละเวลาอันมีค่าของ CEO บริษัท minimore มาร่วมสนุกไปด้วยกัน 😝 ไว้ยังไงถ้าปีหน้ายังฟิตอยู่ไว้มาด้วยกันอีกนะ
-
Demaine, E. D., Demaine, M. L., Minsky, Y. N., Mitchell, J. S., Rivest, R. L., & Pǎtraşcu, M. (2014). Picture-hanging puzzles. Theory of Computing Systems, 54(4), 531-550. ↩
-
Rosenkrantz, D. J., Stearns, R. E., & Lewis, P. M. (1974, October). Approximate algorithms for the traveling salesperson problem. In Switching and Automata Theory, 1974., IEEE Conference Record of 15th Annual Symposium on (pp. 33-42). IEEE. ↩

author