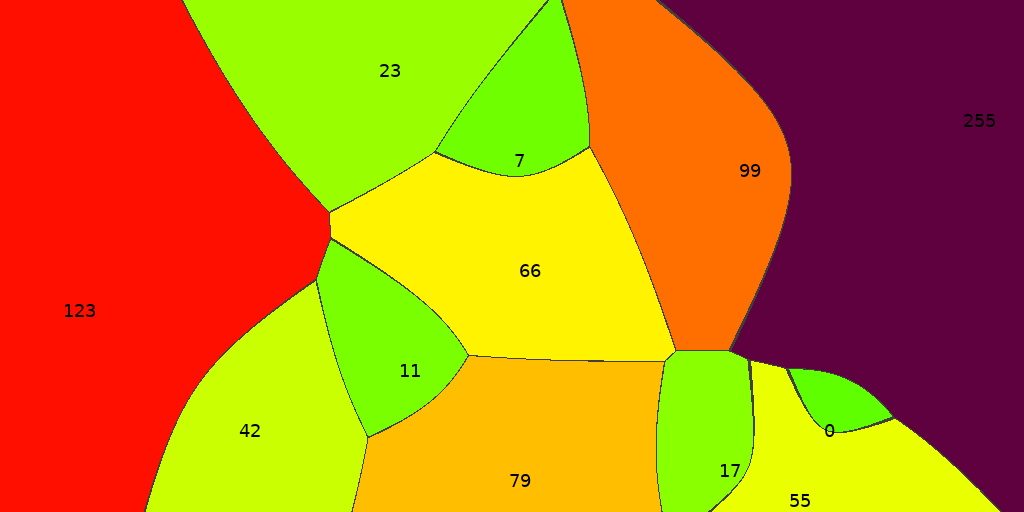
แผนภาพ Voronoi ที่เส้นขอบเป็นไฮเพอร์โบลา

Wednesday, May 13, 2020, 10:24 AM

เคยเขียนถึงแผนภาพ Voronoi ไปบ้าง (1, 2) ว่าแนวคิดมันคือการแบ่งแผนที่ออกเป็นเซลล์ เพื่อให้ข้อมูลว่าแต่ละเซลล์อยู่ใกล้กับจุดตั้งต้นจุดไหนมากที่สุด (มองจุดตั้งต้นเป็นสถานีดับเพลิงก็ได้ว่าจะแบ่งพื้นที่กันยังไงให้เวลาไฟไหม้แล้วรถดับเพลิงไปถึงจุดเกิดเหตุไวที่สุด)

อัลกอริทึมสำหรับคำนวณหาแผนภาพ Voronoi นั้นมีอยู่มากมาย แต่วิธีที่นำมาอธิบายได้ง่ายที่สุดคือการสร้างวงกลมล้อมรอบแต่ละสถานี แล้วขยายขนาดวงกลมออกมาเรื่อยๆ จนวงกลมชนกัน จุดที่ชนก็จะเป็นขอบเขตของแต่ละเซลล์ที่แต่ละสถานีต้องรับผิดชอบ ซึ่งเส้นขอบนี้จะเป็นเส้นตรงภายใต้เงื่อนไขที่ว่าแต่ละสถานีเริ่มขยายวงกลมพร้อมกันและขยายด้วยอัตราเร็วเท่ากัน

แล้วถ้าวงกลมที่ล้อมรอบแต่ละสถานีมีจุดเริ่มต้นขยายตัวไม่พร้อมกันหละ (เช่น บางสถานีที่เมื่อได้ข่าวไฟไหม้แล้วสามารถตระเตรียมรถดับเพลิงให้ออกปฏิบัติงานได้เร็วก่อนสถานีอื่น) เช่นนี้แล้วขอบของแต่ละเซลล์จะมีหน้าตาเปลี่ยนแปลงไปเป็นอย่างไร?

ตัวอย่างแผนภาพ Voronoi แบบที่แต่ละจุดตั้งต้นเริ่มขยายวงกลมล่วงหน้าไปก่อนไม่รอเริ่มพร้อมกัน

ปัญหานี้เป็นหนึ่งในปัญหาที่แตกหน่องอกงามออกมา โดยมันมีชื่อเฉพาะว่าแผนภาพ Voronoi ที่ถูกเพิ่มน้ำหนักด้วยการบวก (additively weighted Voronoi diagram) ซึ่งสปอยล์คำตอบตรงนี้ก่อนเลยว่า ขอบเซลล์ที่ได้จะเป็นเส้นโค้งแบบไฮเพอร์โบลา!

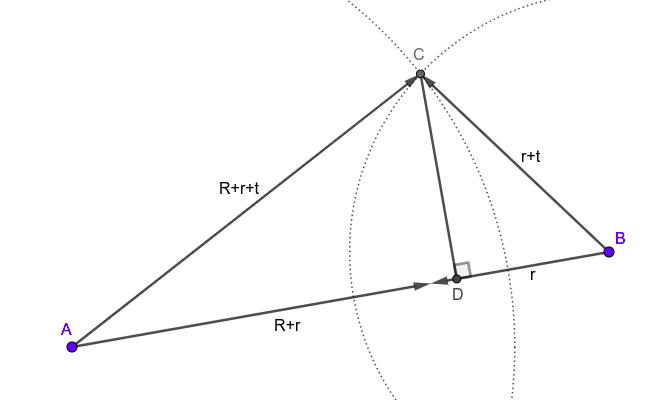
พิจารณาสถานี $A$ กับ $B$ ซึ่งสถานี $A$ เริ่มต้นขยายวงกลมไปก่อนแล้วด้วยขนาด $R$ หน่วย และทั้งสองสถานีต้องขยายวงกลมเพิ่มอีก $r$ หน่วย วงกลมทั้งสองถึงจะมาชนกันที่จุดขอบระหว่างเซลล์จุดแรก หากสนใจจุด $C$ ซึ่งเป็นจุดขอบเมื่อขยายวงกลมเพิ่มไปอีก $t$ หน่วย คำถามคือตำแหน่งของจุด $C$ จะอยู่ ณ พิกัดใด?

สามเหลี่ยมสำหรับวิเคราะห์ปัญหานี้

ดูเผินๆ เหมือนจะคำนวณตำแหน่ง $C$ ได้ยากมาก แต่เราสามารถเริ่มต้นที่การลากเส้นผ่านจุด $C$ ไปตั้งฉากกับ $\overset{―}{A B}$ เพื่อสร้างจุดตัด $D$ ขึ้นมา ซึ่งก็คือเราจะได้ว่า $\overset{―}{A B} = \overset{―}{A D} + \overset{―}{B D}$

นอกจากนี้ เรายังจะได้สมบัติพื้นฐานของสามเหลี่ยมมุมฉาก $△ A D C$ และ $△ B D C$ มาใช้อีกด้วย คือ

\begin{aligned} {\overset{―}{A C}}^{2} & = {\overset{―}{A D}}^{2} + {\overset{―}{C D}}^{2} \\ {\overset{―}{B C}}^{2} & = {\overset{―}{B D}}^{2} + {\overset{―}{C D}}^{2} \end{aligned}

ซึ่งจะทำให้ได้ว่า

\begin{aligned} {\overset{―}{A C}}^{2} - {\overset{―}{A D}}^{2} & = {\overset{―}{B C}}^{2} - {\overset{―}{B D}}^{2} \\ = {\overset{―}{B C}}^{2} - {(\overset{―}{A B} - \overset{―}{A D})}^{2} \\ = {\overset{―}{B C}}^{2} - ({\overset{―}{A B}}^{2} - 2 \overset{―}{A B} \cdot \overset{―}{A D} + {\overset{―}{A D}}^{2}) \\ = {\overset{―}{B C}}^{2} - {\overset{―}{A B}}^{2} + 2 \overset{―}{A B} \cdot \overset{―}{A D} - {\overset{―}{A D}}^{2} \end{aligned}

ย้ายข้างและจัดรูป ก็จะได้คำตอบ

\overset{―}{A D} = \frac{{\overset{―}{A B}}^{2} + {\overset{―}{A C}}^{2} - {\overset{―}{B C}}^{2}}{2 \overset{―}{A B}}

เมื่อรู้ $\overset{―}{A D}$ ก็ง่ายแล้ว เพราะย้อนกลับไปใช้พีทาโกรัสหา $\overset{―}{C D}$ โดยตรงได้ทันที

\overset{―}{C D} = \pm \sqrt{{\overset{―}{A C}}^{2} - {\overset{―}{A D}}^{2}}

ตอนนี้เพื่อความง่ายในการวิเคราะห์ต่อ สมมติให้ $\overset{―}{A B}$ ขนานกับแกน $X$ โดยให้ $A = (\frac{- R - 2 r}{2}, 0)$ และ $B = (\frac{R + 2 r}{2}, 0)$ แล้วแทนค่าความยาวด้านต่างๆ ลงไปเพื่อหาตำแหน่งของ $C = (x, y)$ เริ่มจากหาตำแหน่งในแกน $X$ ก่อน ก็จะได้ว่า

\begin{aligned} x & = \frac{(R + 2 r)^{2} + (R + r + t)^{2} - (r + t)^{2}}{2 (R + 2 r)} \\ = r + R (1 + \frac{t}{R + 2 r}) \\ t & = (R + 2 r) (\frac{x - r}{R} - 1) \end{aligned}

และเมื่อหาตำแหน่งในแกน $Y$ ก็จะได้

\begin{aligned} y^{2} & = (R + r + t)^{2} - {(\frac{R}{2} + r + x)}^{2} \\ = {(\frac{R^{2} + 2 x R + 4 x r}{2 R})}^{2} - {(\frac{R^{2} + 2 r R + 2 x R}{2 R})}^{2} \\ = \frac{1}{R^{2}} (4 x^{2} r R + 4 x^{2} r^{2} - r R^{3} - r^{2} R^{2}) \end{aligned}

ถึงจะได้ข้อมูลตำแหน่งมาครบก็อาจจะยังมองไม่ชัดถึงหน้าตาสมการว่าเป็นไฮเพอร์โบลาได้อย่างไร แต่ถ้าอดทนจัดรูปต่อไปอีกหน่อยก็จะเห็นว่าสมการข้างต้นมันสามารถกลายเป็น